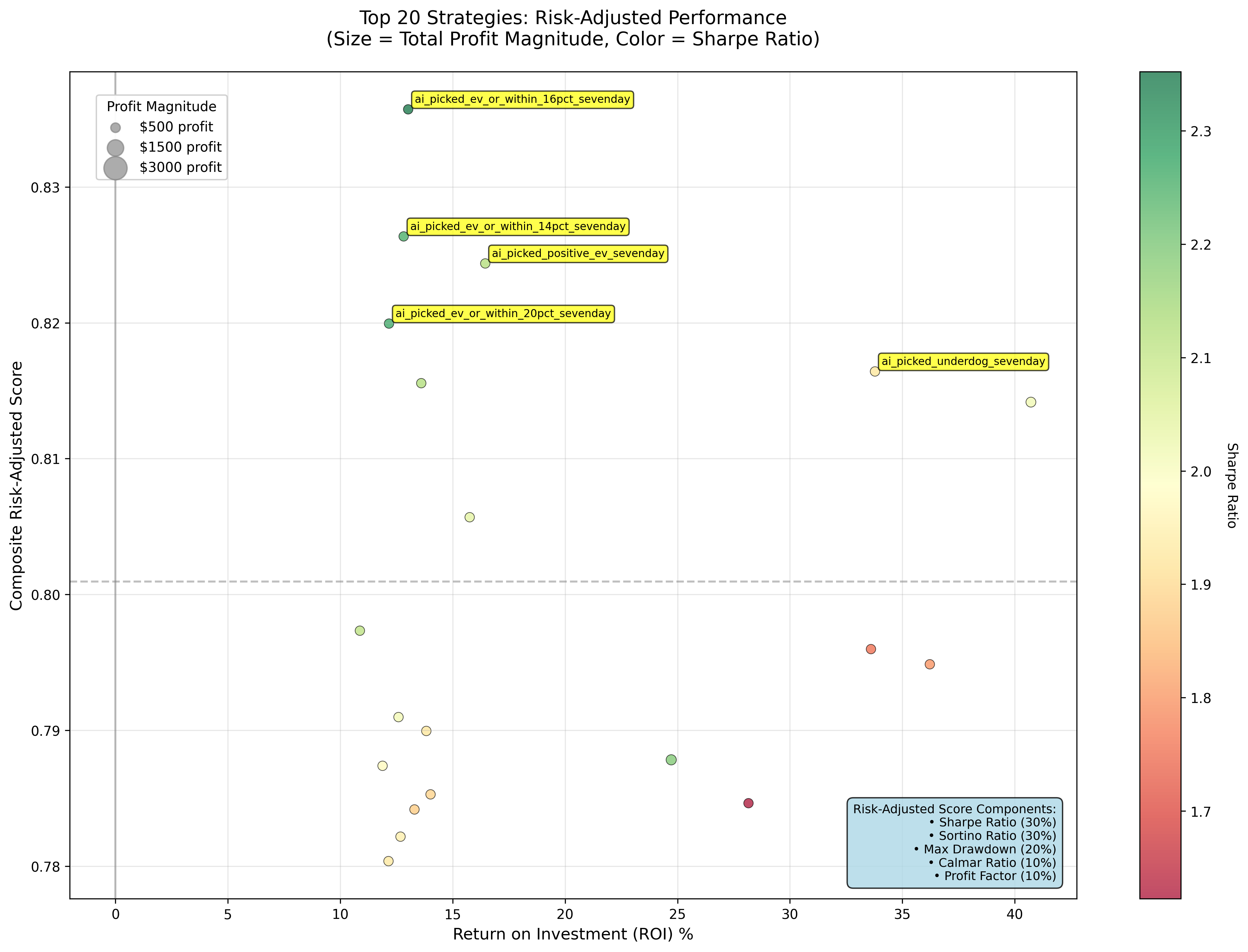
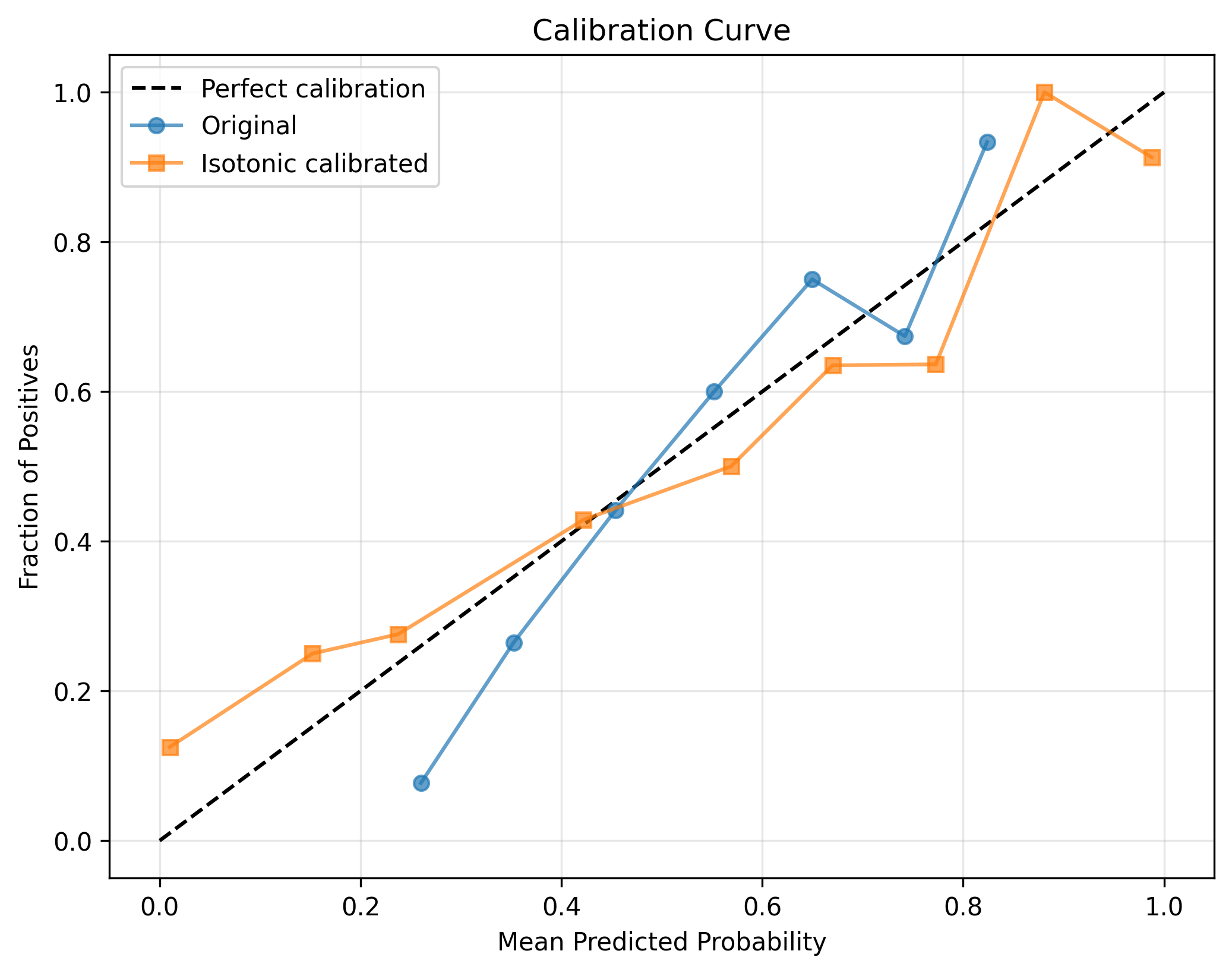
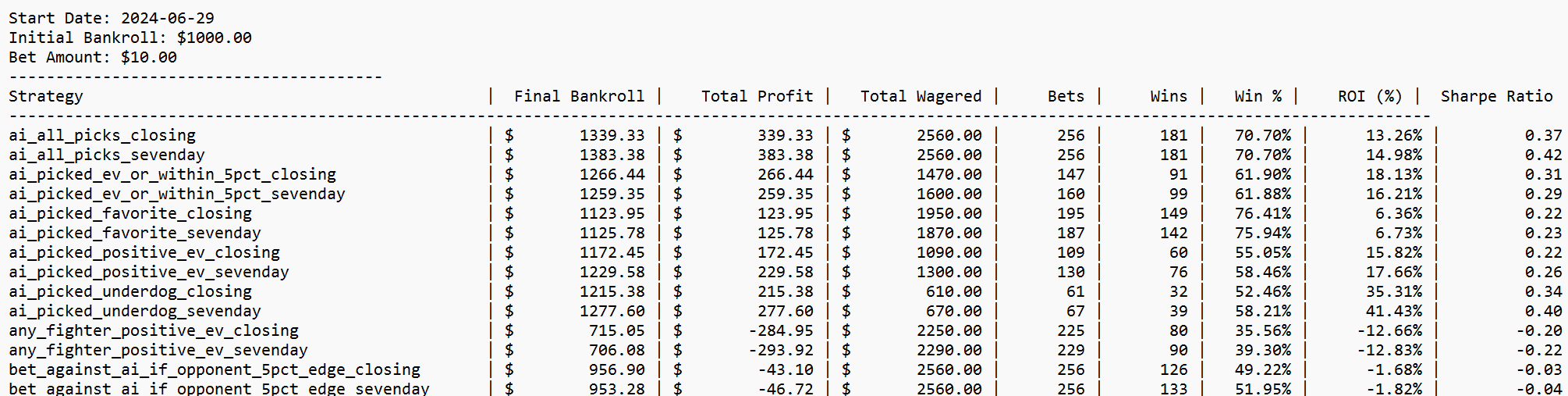
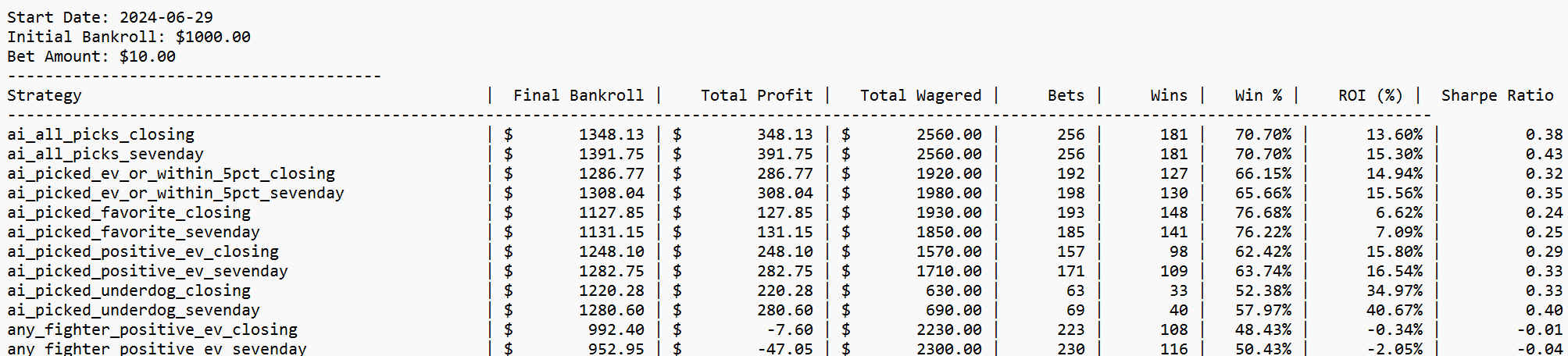
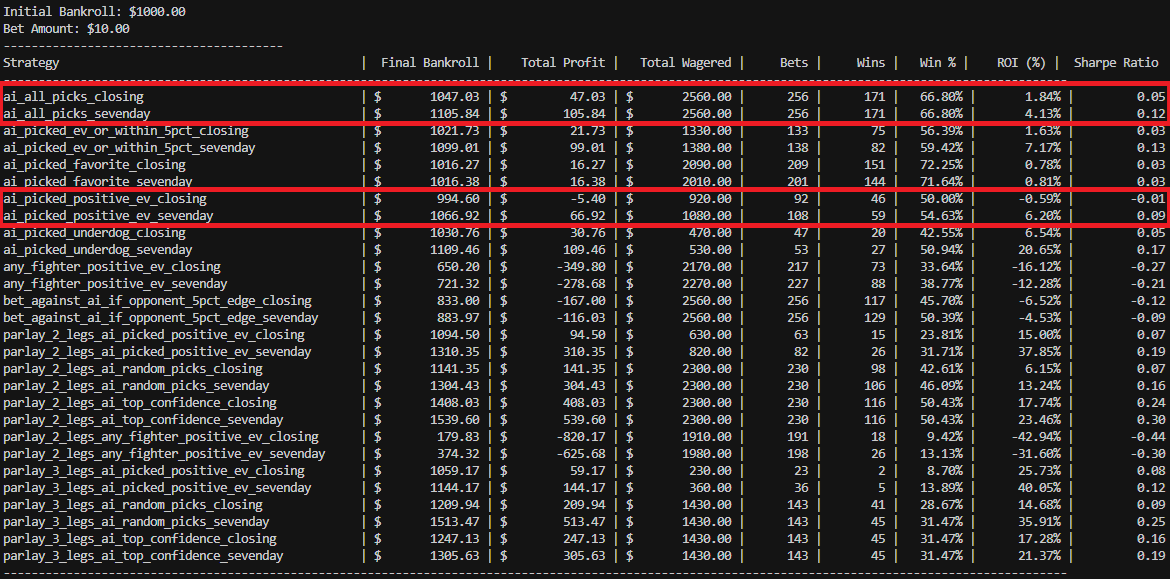
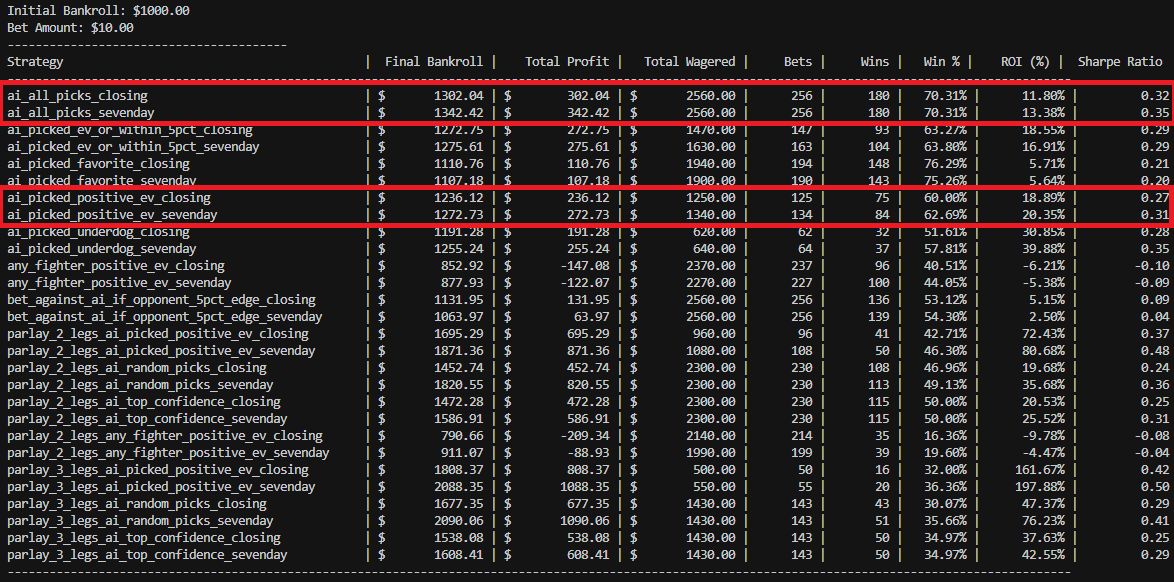
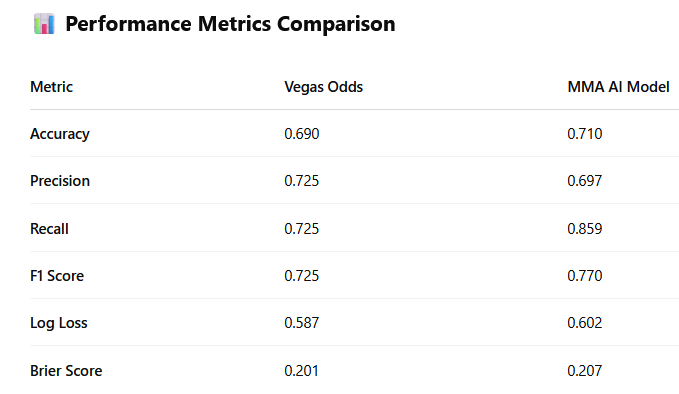
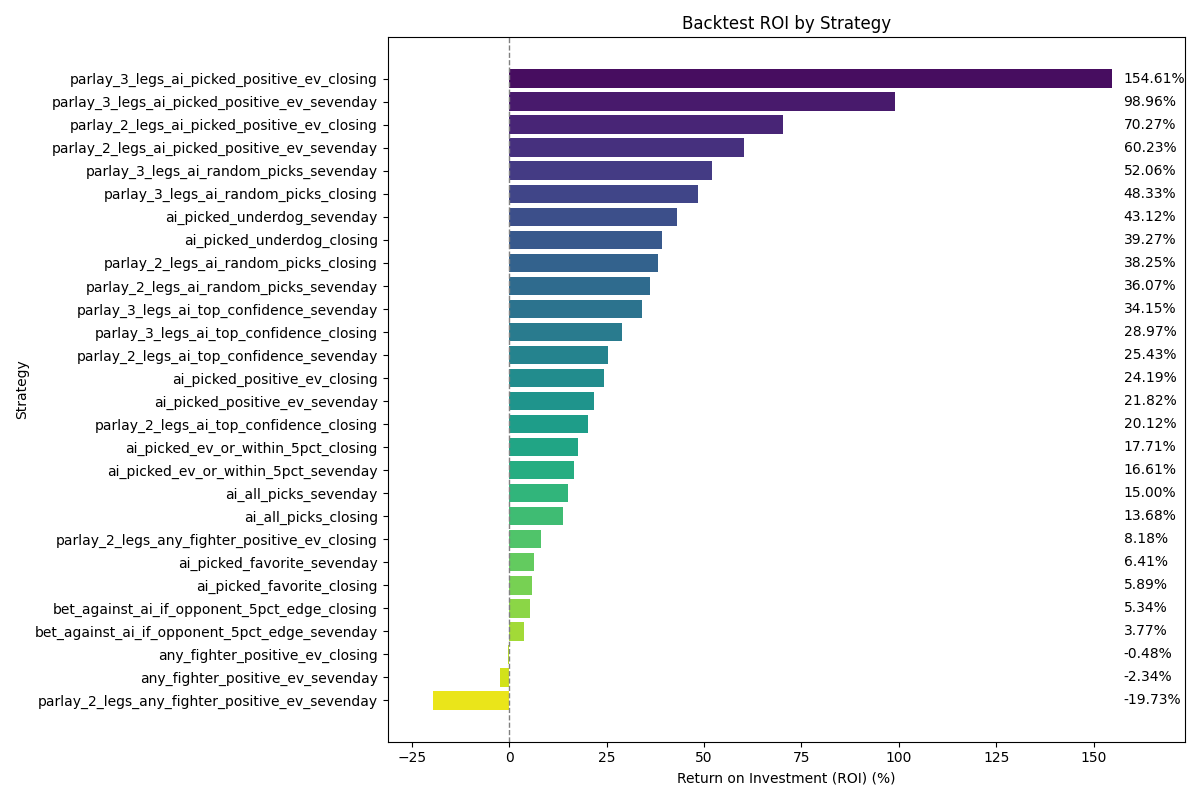
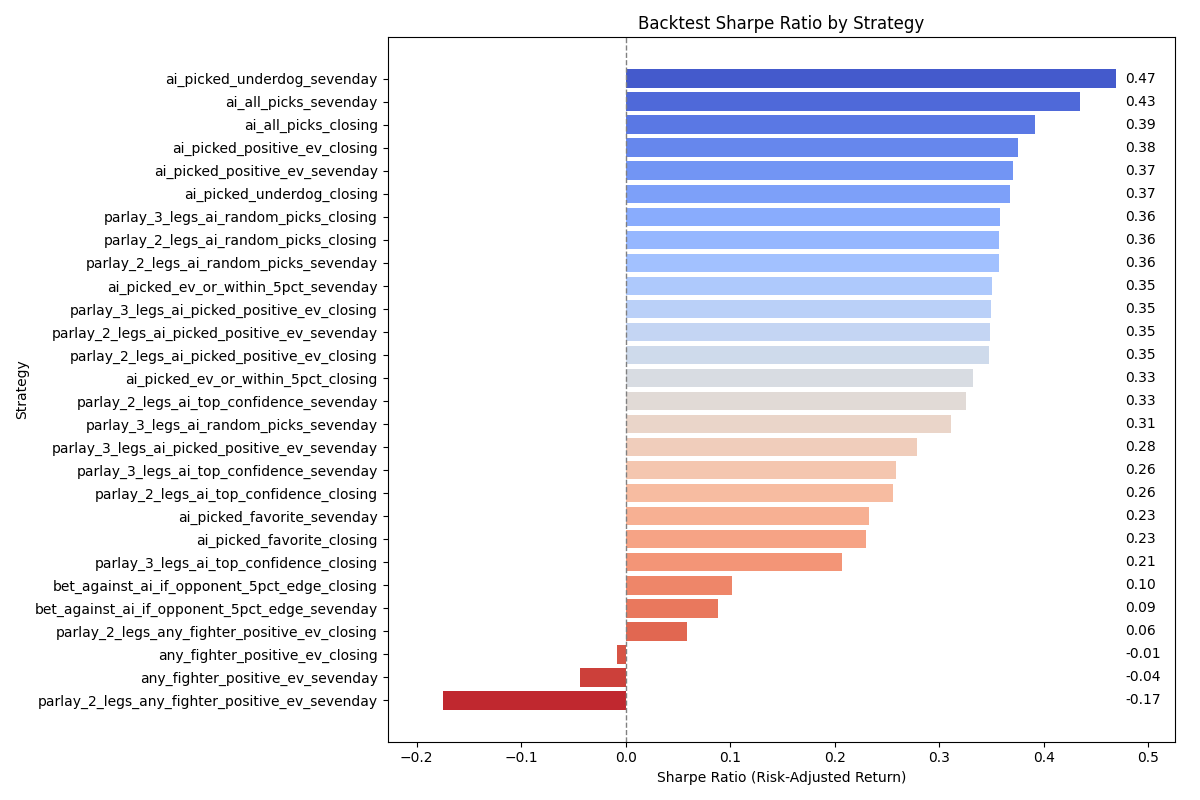
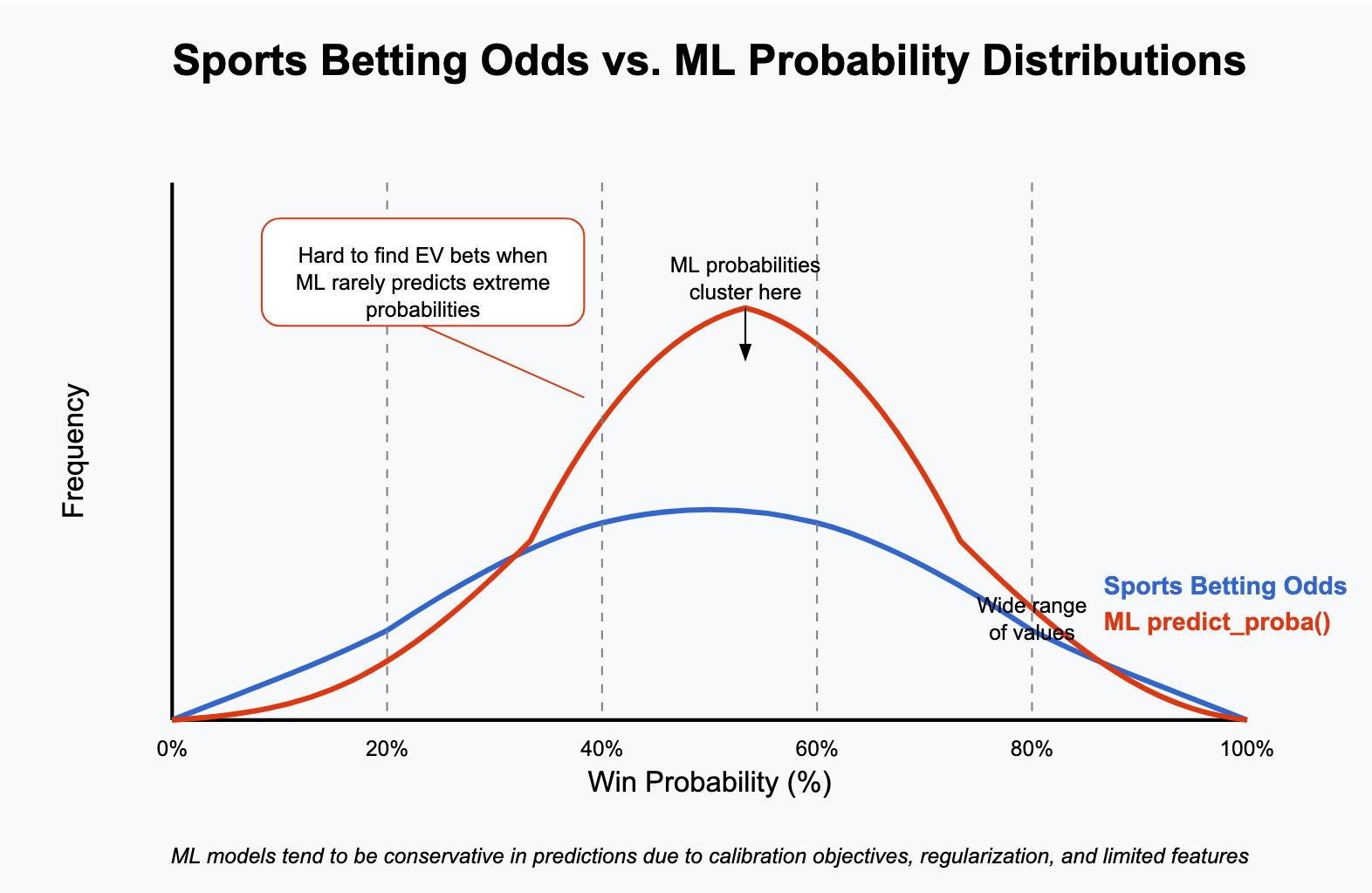
I gave AI access to my odds database and told it to do analysis on the data. This is the result. I double checked most of the results but bear in mind there might still be minor discrepancies and also note that my odds data is not 100% comprehensive, I think I have about 70%(?) coverage of all the fights in 2024/2025.

The Core Paradox

When we analyze betting markets, we typically expect efficiency and accuracy to go hand-in-hand. More efficient markets should mean better predictions. But 2025 broke that assumption.

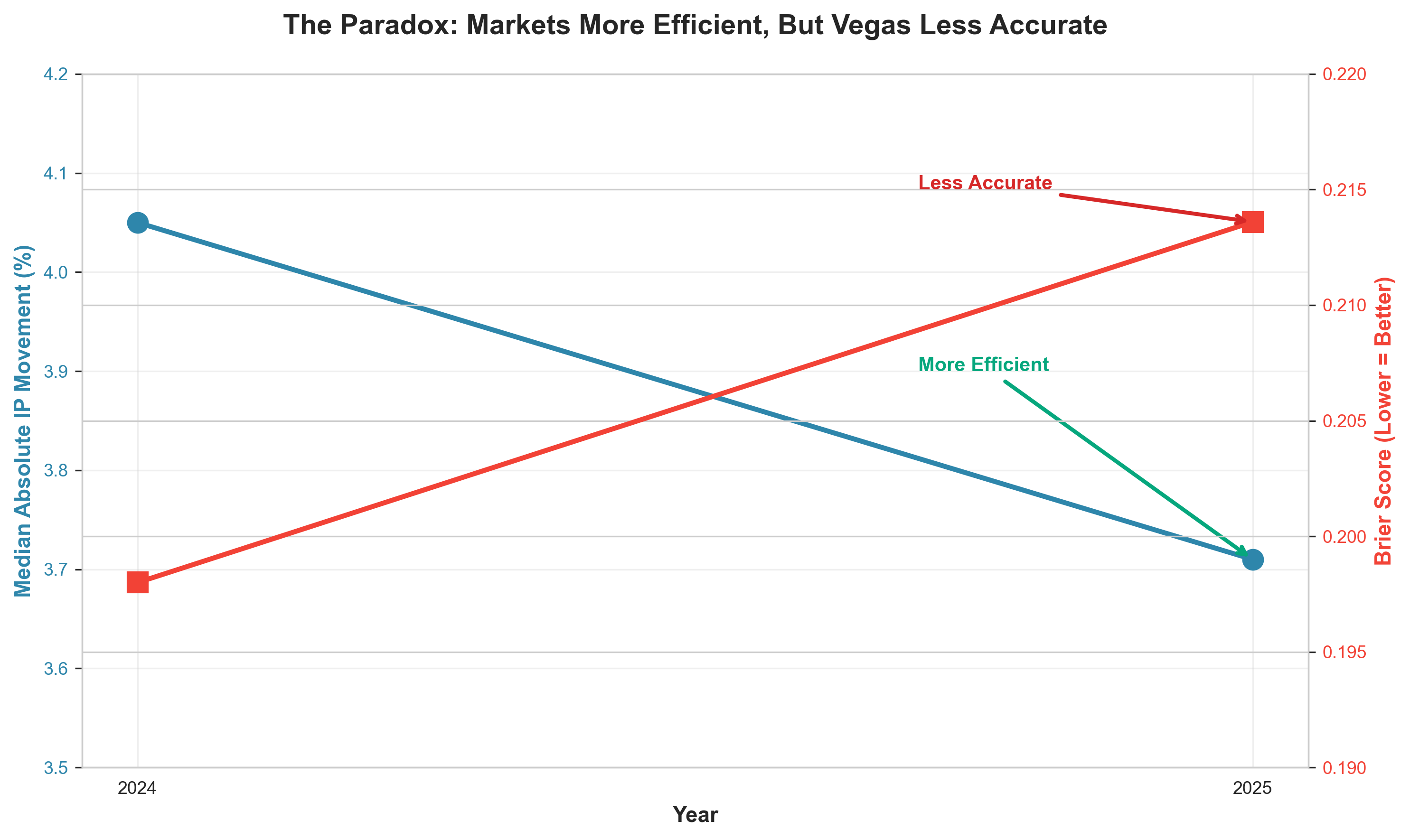
Figure 1: Markets became more efficient (median movement decreased), but Vegas accuracy declined (Brier score increased)

Where Did Vegas Go Wrong?

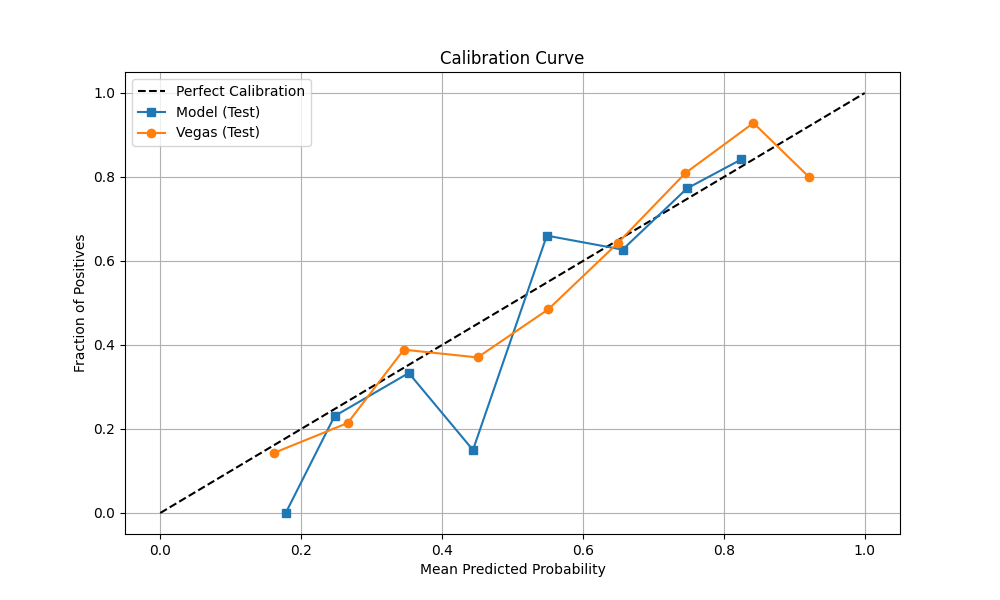
To understand why Vegas became less accurate despite more efficient markets, we need to look at calibration—how well Vegas's implied probabilities matched actual outcomes.

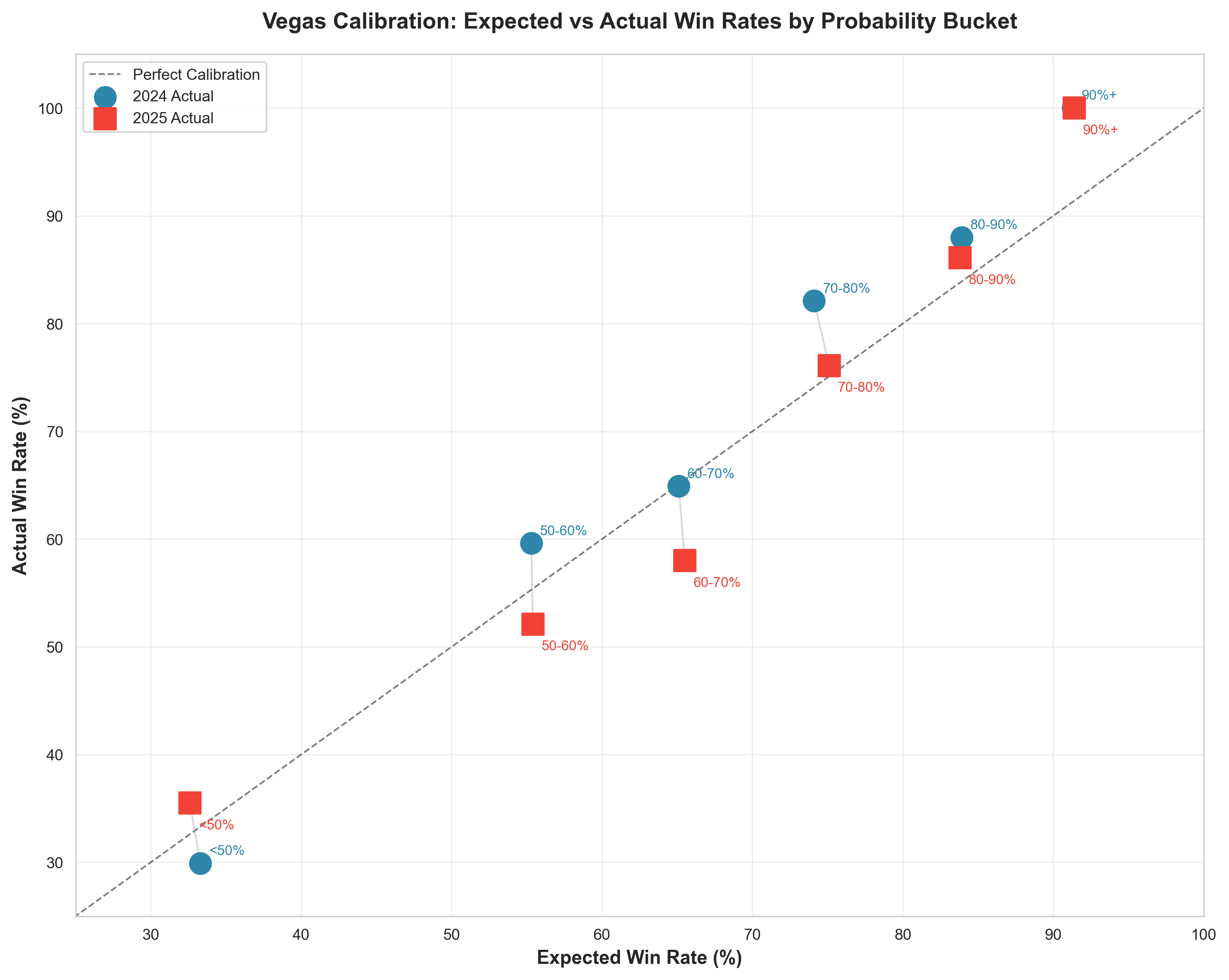
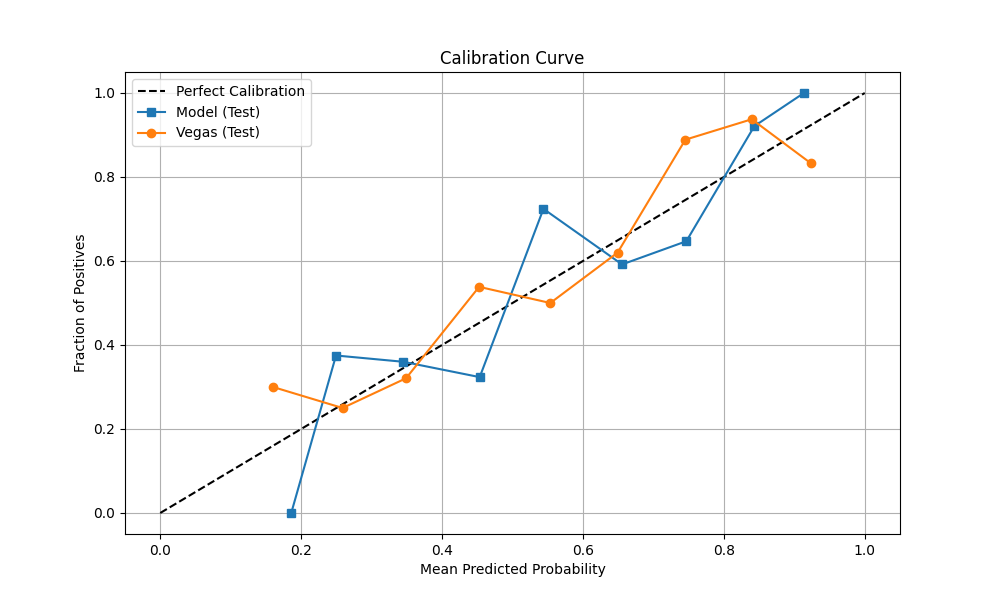
Figure 2: Expected vs Actual Win Rates by Probability Bucket. Points on the diagonal line = perfect calibration

The calibration plot reveals a critical issue: Vegas significantly underestimated favorites in 2025, particularly in the 60-70% probability bucket. In 2024, Vegas was well-calibrated for this range (64.9% actual vs 65.1% expected). But in 2025, favorites in this bucket won only 58.0% of the time when Vegas expected 65.5%—a 7.5 percentage point miss.

Sharp Money Influence Declining

One explanation for more efficient markets is that sharp bettors (professional bettors with sophisticated models) had less influence in 2025. When sharp money moves lines significantly, it creates volatility. Less sharp influence means tighter, more stable lines.

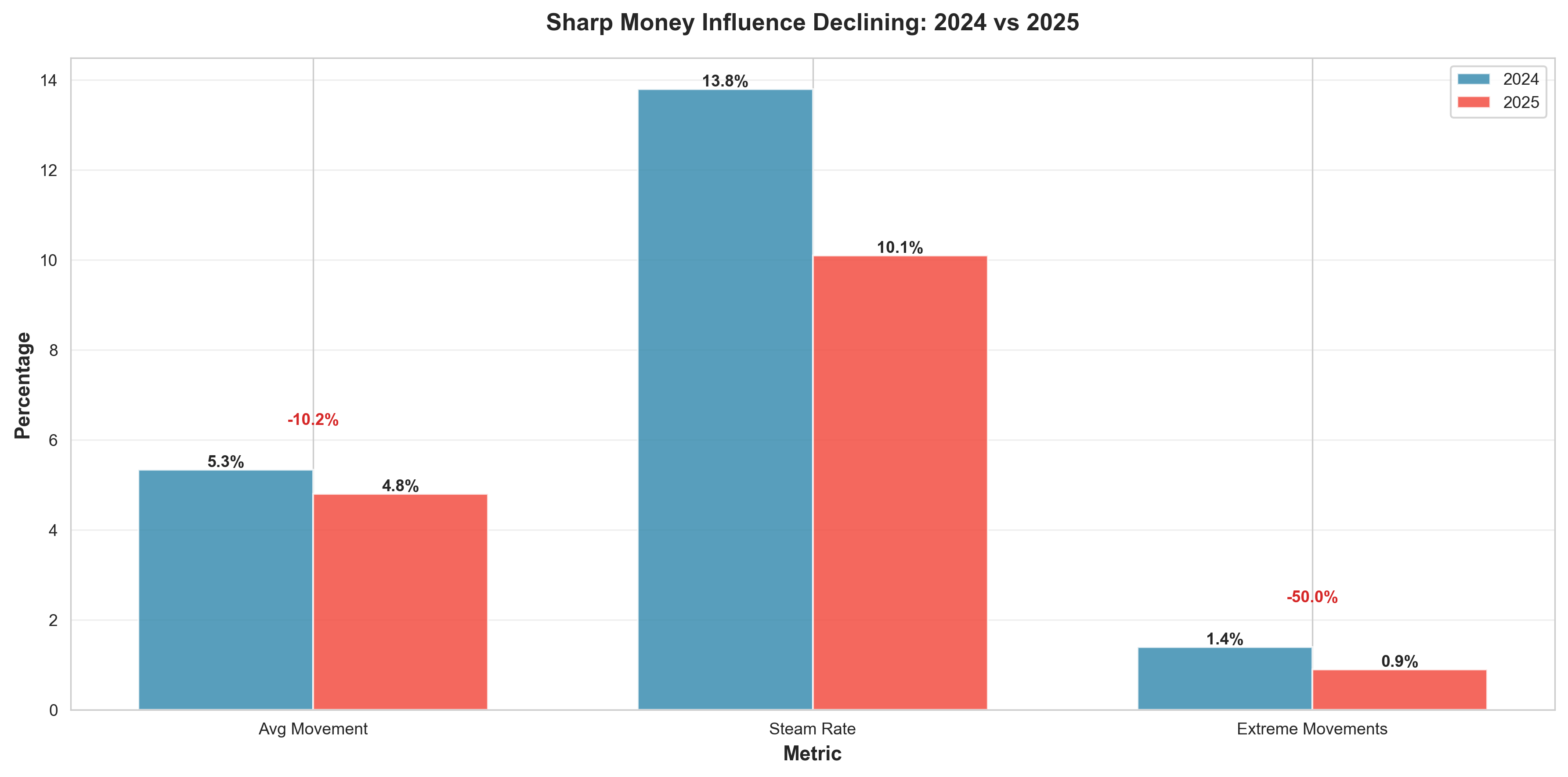
Figure 3: Sharp money influence declined across all metrics in 2025

• Average Movement: Decreased from 5.34% to 4.80% (-10.2%)
• Steam Bets: Decreased from 13.8% to 10.1% (-3.7 percentage points)
• Extreme Movements (>20%): Decreased from 1.4% to 0.9% (-50%)

"Steam bets" are rapid, coordinated line movements that typically indicate sharp money entering the market. The decline in steam bets suggests either:

1. Sharps found fewer value opportunities (markets already efficient)
2. Sharps were less active in 2025
3. Public bettors got smarter, reducing the need for sharp correction

Public Getting Smarter: Favorites Moving Against Public Money

One of the most interesting trends in 2025 was the increase in favorites whose odds worsened (got longer) despite being the public favorite. This is a key indicator of sharp money betting against public sentiment.

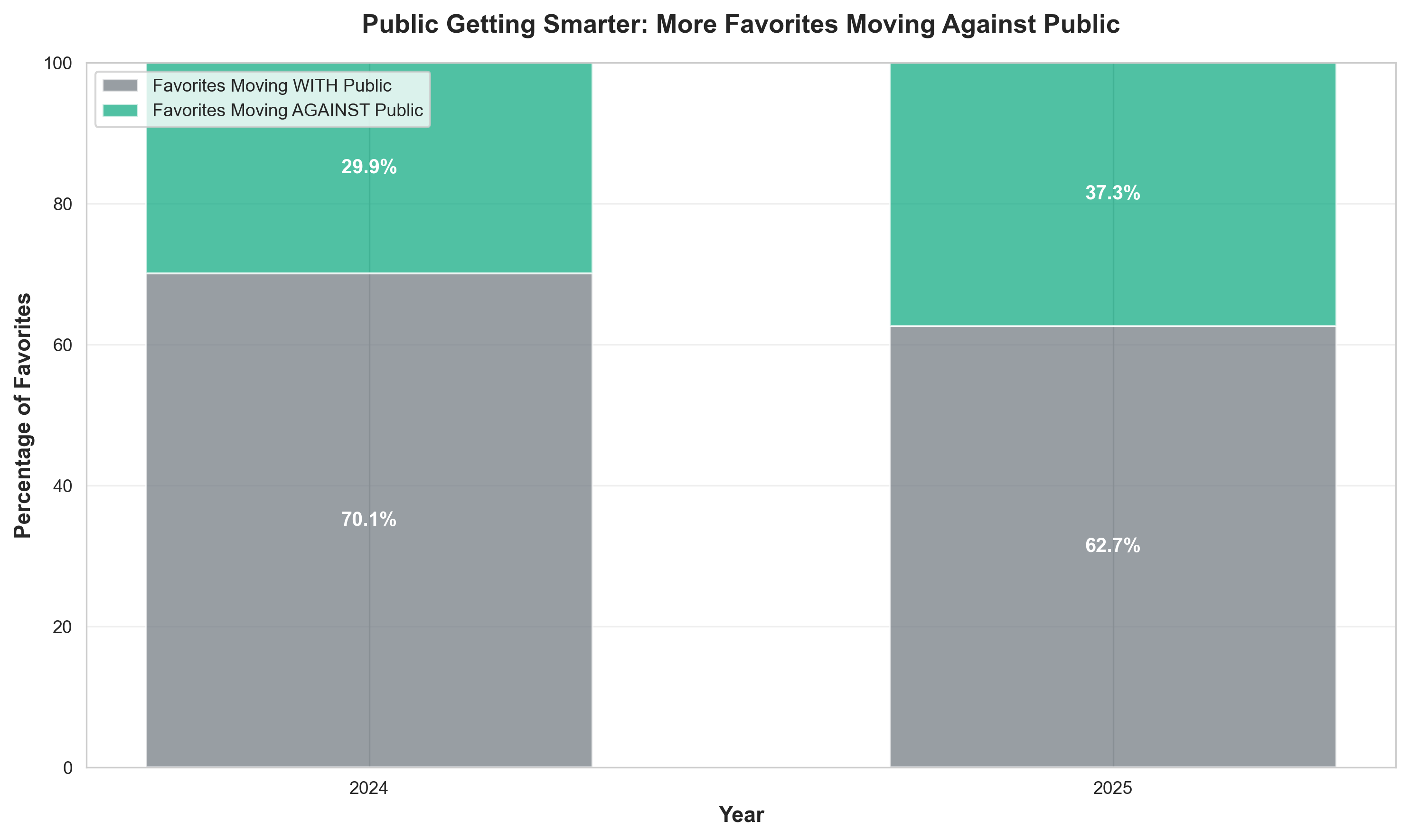
Figure 4: Percentage of favorites moving with vs against public money

In 2024, 29.9% of favorites moved against public money. In 2025, this increased to 37.3%—a +7.4 percentage point increase. This suggests sharp bettors found more value betting against favorites, or that public bettors were less accurate in their initial assessments.

Temporal Patterns: When Steam Happens

Not all months are created equal when it comes to betting activity. February and October 2025 saw the highest steam bet rates, suggesting these months had the most sharp betting activity or the most mispriced lines.

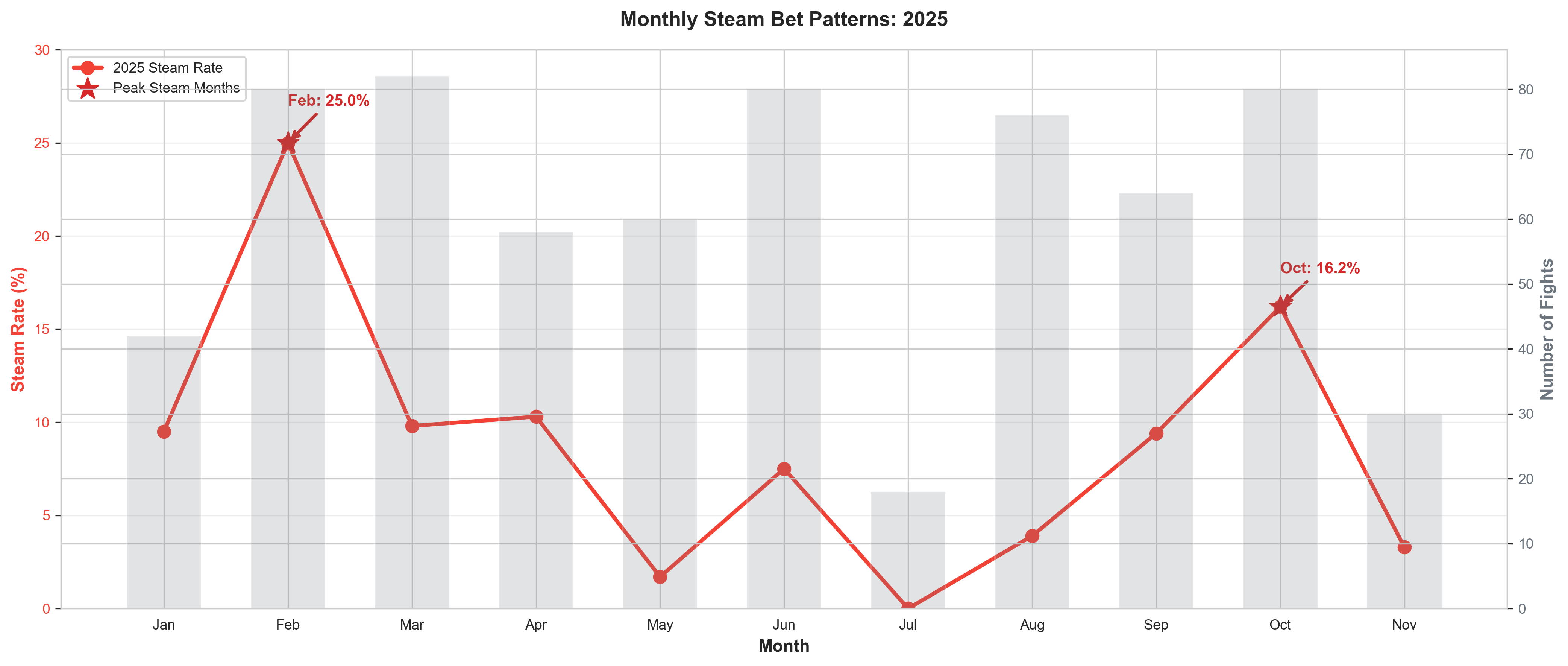
Figure 5: Monthly steam bet rates in 2025, with fight counts shown in background

February 2025: 25.0% steam rate—the highest of the year. This suggests significant sharp activity or major line corrections during this period.

October 2025: 16.2% steam rate—the second highest. This could indicate high-profile fights with significant betting interest or mispriced lines.

July 2025: 0.0% steam rate—the lowest, with only 18 fights. This suggests either very efficient initial pricing or limited sharp interest.

The Biggest Line Movements of 2025

Some fights saw dramatic line movements, indicating significant sharp money or late-breaking information. Here are the most extreme cases:

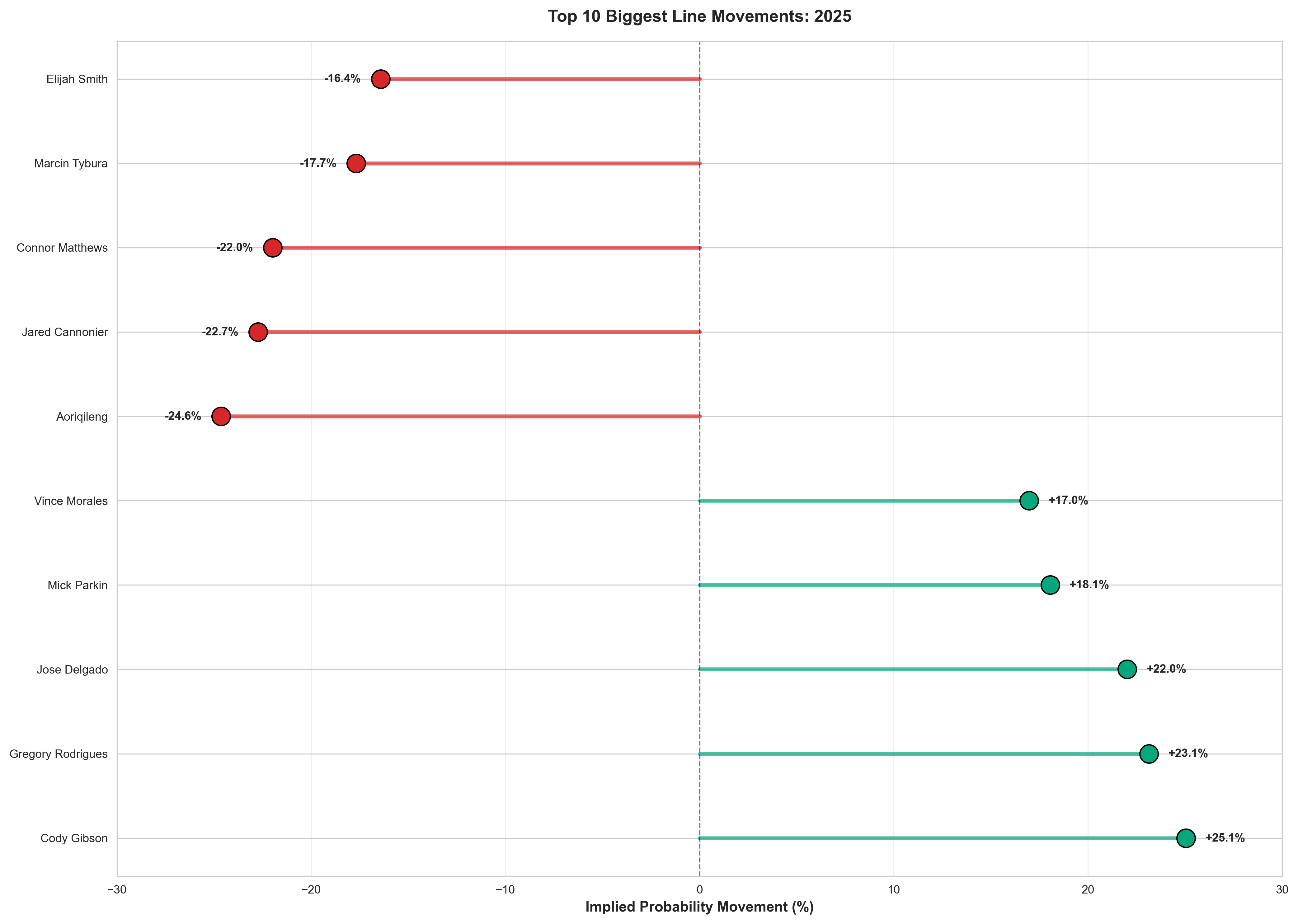
Figure 6: Top 10 biggest implied probability movements in 2025

Biggest Positive Movement: Cody Gibson saw his implied probability increase by +25.05% (from 40.8% to 65.9%) against Aoriqileng. This massive move suggests sharp money heavily favored Gibson, or late-breaking information changed the assessment.

Biggest Negative Movement: Aoriqileng (in the same fight) saw his implied probability decrease by -24.65% (from 63.0% to 38.3%). This is the flip side of Gibson's movement—when one fighter's odds improve dramatically, their opponent's must worsen.

Opening vs Closing: Market Learning

One way to measure market efficiency is to compare opening odds (the initial line) to closing odds (the final line). If markets are learning and incorporating information, closing odds should be more accurate than opening odds.

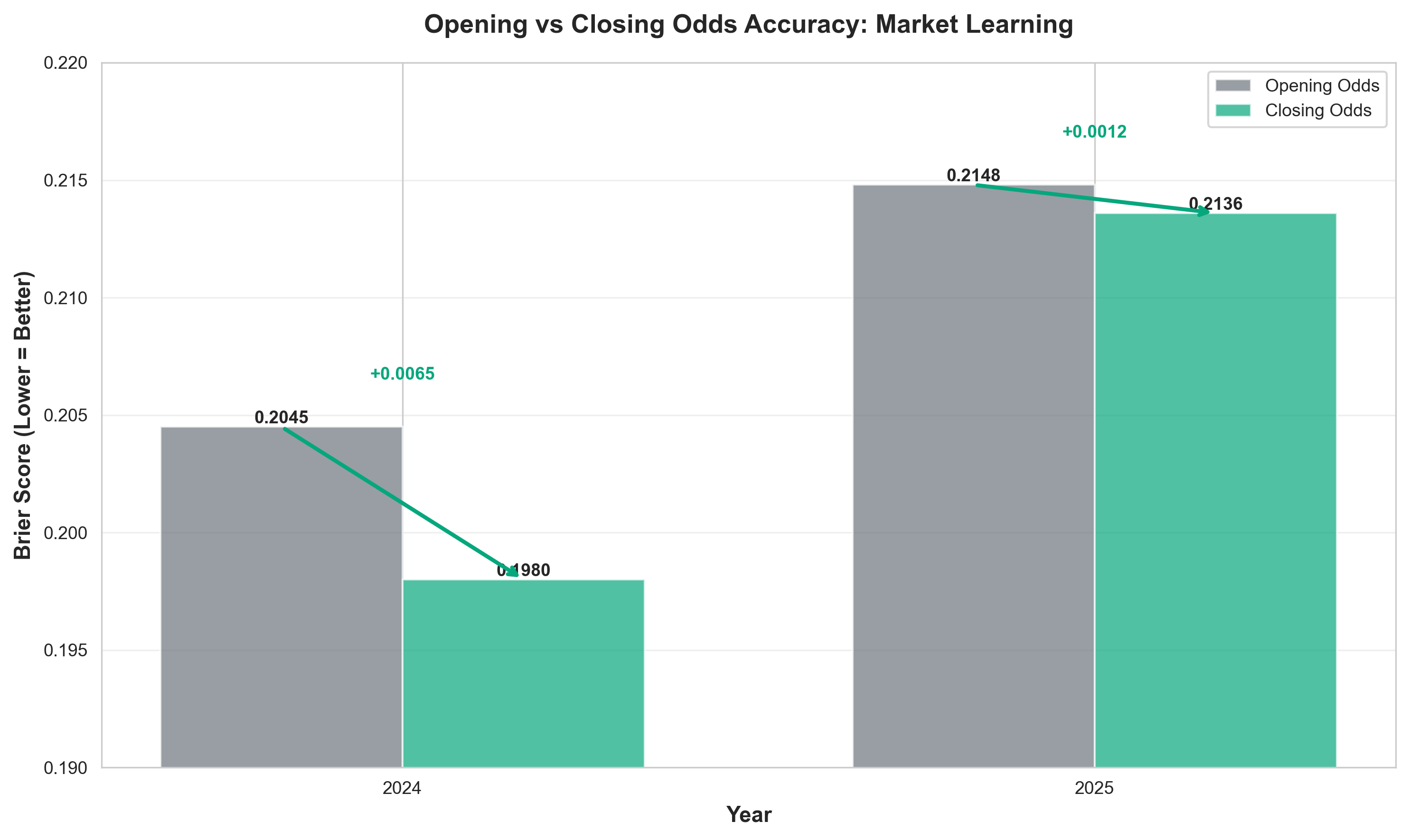
Figure 7: Brier scores for opening vs closing odds. Lower Brier score = better accuracy

In both years, closing odds were more accurate than opening odds, confirming that markets do learn and incorporate information. However, the improvement was much smaller in 2025:

• 2024: Opening Brier 0.2045 → Closing Brier 0.1980 (+0.0065 improvement)
• 2025: Opening Brier 0.2148 → Closing Brier 0.2136 (+0.0012 improvement)

This suggests that in 2025, opening lines were already closer to optimal, leaving less room for improvement. However, the overall accuracy was still worse than 2024, indicating a systematic calibration issue rather than just initial mispricing.

Fighter-Specific Storylines

Some fighters consistently saw significant line movement, suggesting the market was frequently mispricing their fights or that sharp bettors consistently found value betting on (or against) them.

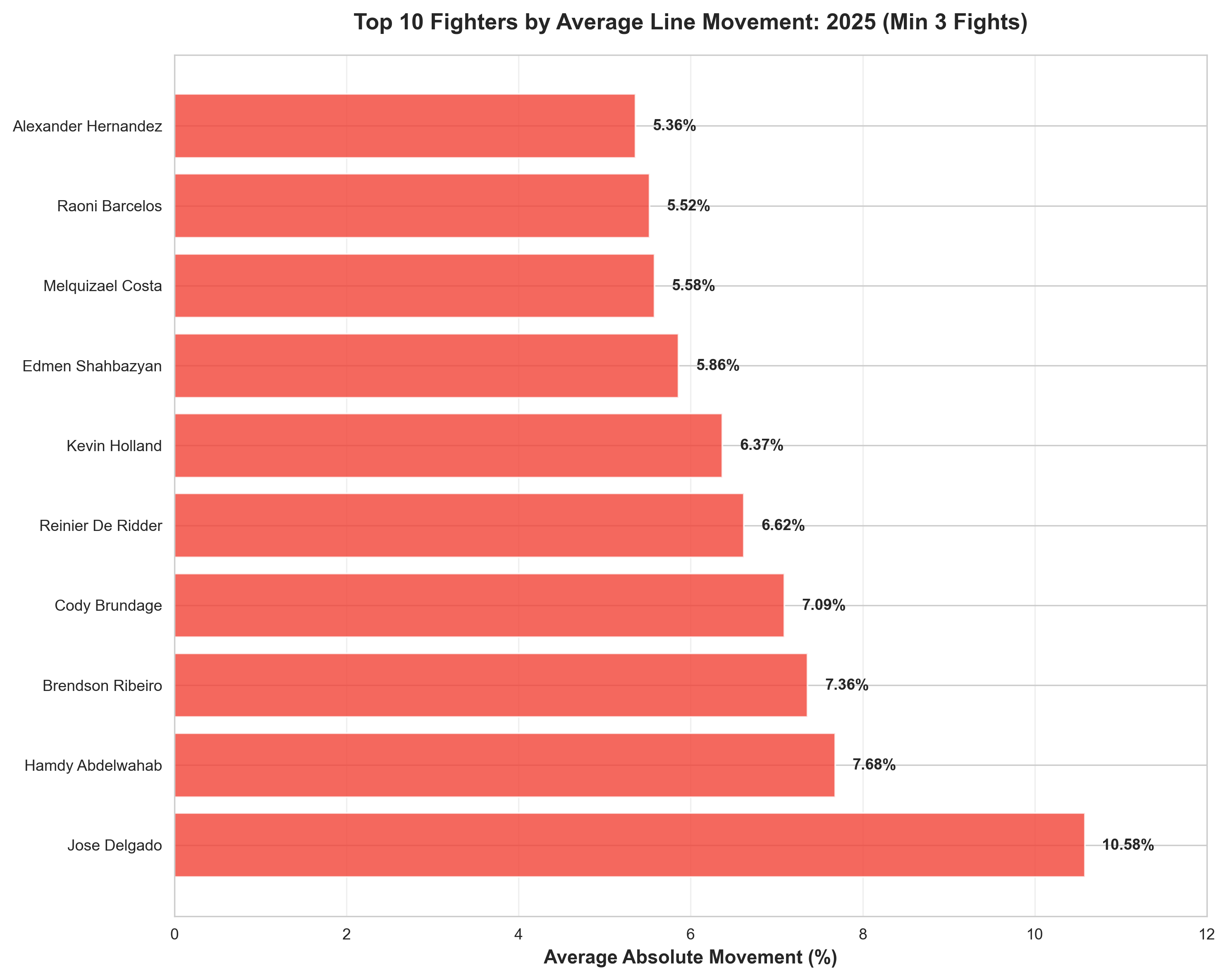
Figure 8: Top 10 fighters by average absolute line movement in 2025 (minimum 3 fights)

Jose Delgado led the pack with an average movement of 10.58% across 3 fights, with odds improving in 2 of those fights. This suggests the market consistently undervalued Delgado initially, and sharp money corrected the line.

Distribution of Movements: Less Extreme Tails

The overall distribution of line movements shifted in 2025, with fewer extreme movements and a tighter distribution around the median.

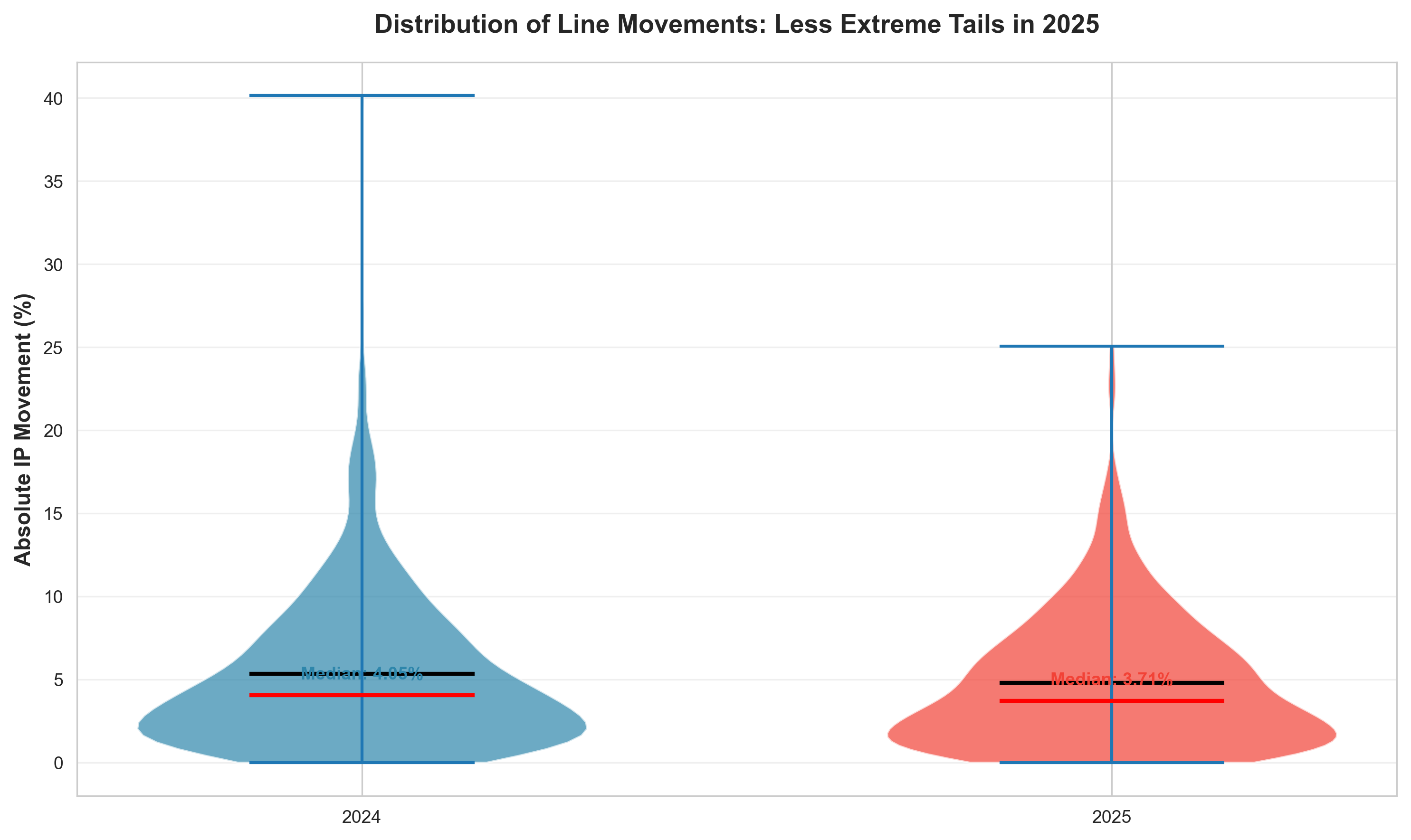
Figure 9: Distribution of absolute line movements. Wider violins = more variation

The violin plot shows that 2025 had a tighter distribution with less extreme tail movements. The median decreased from 4.05% to 3.71%, and the standard deviation decreased from 4.90% to 4.12%. This confirms that markets became more stable and efficient, with fewer dramatic corrections.

Movement vs Accuracy: Individual Fight Analysis

Does more line movement correlate with better or worse accuracy? The scatter plot shows the relationship between absolute movement and prediction error for individual fights.

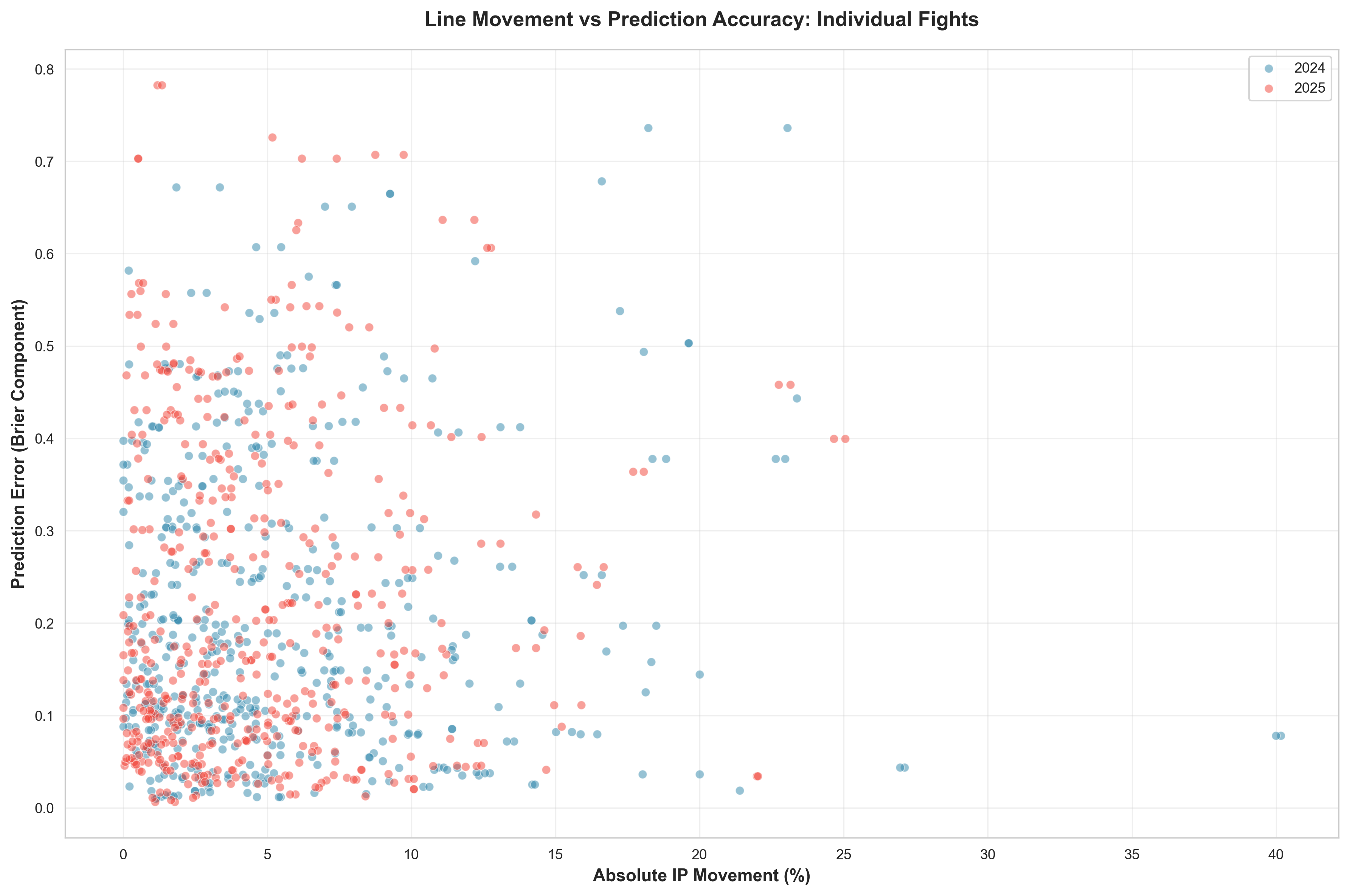
Figure 10: Relationship between line movement and prediction accuracy for individual fights

While there's no strong correlation visible, the plot shows that both years had fights with high movement and low error (sharp corrections that improved accuracy) as well as high movement and high error (corrections that made things worse). This suggests that movement alone doesn't guarantee accuracy—it depends on whether the movement is correcting a mispricing or overreacting to information.

Most Suspicious Fights: Statistical Anomalies

While analyzing the data, we identified fights with patterns that raise statistical eyebrows—combinations of factors that, while not proof of anything nefarious, are worth noting. We created a composite "suspicion score" that combines:

• Prediction Error (30%): How wrong Vegas was about the outcome
• Late Movement (25%): Dramatic odds changes in the final 7 days before the fight
• Heavy Favorite Loss (20%): Favorites with >70% implied probability that lost
• Extreme Favorite Loss (15%): Favorites with >80% implied probability that lost
• Underdog Late Win (10%): Underdogs who won with >5% late movement

Top Suspicious Fights: 2024

Most Suspicious: Kyler Phillips vs Rob Font (October 19, 2024)

• Suspicion Score: 0.8096 (highest of the year)
• Context: Phillips was an 82.4% favorite but lost
• Late Movement: 12.16% movement in final 7 days
• Prediction Error: 0.6784 (Vegas was very wrong)
• Pattern: Extreme favorite loss with significant late movement

Other notable suspicious fights in 2024:

• Javid Basharat vs Aiemann Zahabi (Score: 0.7596) - 85.8% favorite lost
• Mateusz Rebecki vs Diego Ferreira (Score: 0.7536) - 81.6% favorite lost with 8.80% late movement
• Kennedy Nzechukwu vs Ovince Saint Preux (Score: 0.6974) - 83.7% favorite lost

Top Suspicious Fights: 2025

Most Suspicious: Rinya Nakamura vs Muin Gafurov (January 18, 2025)

• Suspicion Score: 0.7231 (highest of the year)
• Context: Nakamura was an 84.1% favorite but lost
• Late Movement: 7.14% movement in final 7 days
• Prediction Error: 0.7072 (Vegas was very wrong)
• Pattern: Extreme favorite loss

Other notable suspicious fights in 2025:

• Josias Musasa vs Carlos Vera (Score: 0.6907) - 85.2% favorite lost
• Oumar Sy vs Alonzo Menifield (Score: 0.6875) - 83.8% favorite lost
• Payton Talbott vs Raoni Barcelos (Score: 0.6523) - 88.4% favorite lost (highest IP favorite to lose)

Patterns in Suspicious Fights

Analyzing the suspicious fights reveals some patterns:

• Heavy favorites losing: Most suspicious fights involve favorites with >80% implied probability losing—these are inherently rare events that Vegas heavily favored.
• Late movement correlation: Many suspicious fights had significant late movement (>5%), suggesting information entered the market close to fight time.
• Underdog wins: Several suspicious fights featured underdogs winning with large late movement, potentially indicating sharp money betting against public sentiment.

Notable: Payton Talbott vs Raoni Barcelos stands out—Talbott was an 88.4% favorite (one of the highest IP favorites in the dataset) but lost. This represents a massive prediction error (0.7823) even though there was minimal late movement (0.16%), suggesting the initial line may have been fundamentally mispriced.

Conclusion: The Precision-Accuracy Paradox

Analysis based on 802 fights in 2024 and 664 fights in 2025, using vigless implied probabilities from closing odds. Data sourced from features.odds table in mma-ai database.

If you're lucky enough to have an NVIDIA RTX 5090 (or any Blackwell architecture GPU), you've probably discovered that getting AutoGluon 1.4.0 to work with it isn't exactly straightforward. The problem? AutoGluon requires older PyTorch versions, but the RTX 5090 needs PyTorch Nightly with CUDA 13 support. This guide will walk you through a "Frankenstein" installation that makes these incompatible pieces work together.

Prerequisites

Before we dive in, make sure you have:

• Python 3.10-3.12 (Python 3.12.4 recommended)
  • Note: Python 3.10-3.12 required for PyTorch Nightly (RTX 5090 setup)
  • AutoGluon 1.4.0 requires Python >=3.9,<3.13
  • If using uv (recommended), Python will be installed automatically - no need to install it separately
• PostgreSQL database
• uv package manager (required for RTX 5090 setup)
• NVIDIA GPU (RTX 5090 / Blackwell supported with special setup)

⚡ Extreme Performance Setup (RTX 5090 / Blackwell)

⚠️ CRITICAL NOTE: This setup uses a "Frankenstein" environment to force AutoGluon (which normally requires older PyTorch) to run on the RTX 5090 (which requires PyTorch Nightly/CUDA 13).

Do NOT run uv sync after completing these steps. Doing so will revert your packages and break the environment.

Step 1: Configure Base Dependencies

Ensure your pyproject.toml includes torch (configured for Nightly) but EXCLUDES autogluon.

Install the base environment (Layer 1): This installs Python 3.12, PyTorch Nightly (CUDA 13), and standard tools (pandas, numpy, etc.).

uv sync

Step 2: The "Sideload" Installation

We must manually force-install AutoGluon without dependencies to bypass the PyTorch version check, then manually install the missing libraries.

Force Install AutoGluon:

uv pip install "autogluon[tabarena]==1.4.0" --no-deps

Install Required Sub-Dependencies:

These are the libraries AutoGluon needs to run that we skipped in step 2.

uv pip install autogluon-common==1.4.0 autogluon-core==1.4.0 autogluon-features==1.4.0 autogluon-tabular==1.4.0 autogluon-multimodal==1.4.0 tabpfn

Install Manual Fixes:

These libraries are required for the prediction pipeline and specific model architectures.

uv pip install einx loguru networkx psutil defusedxml scipy

Step 3: Verification

Run this command to confirm your environment sees the RTX 5090:

uv run python -c "import torch; print(f'CUDA Available: {torch.cuda.is_available()}'); print(f'Device: {torch.cuda.get_device_name(0)}'); print(f'Torch Version: {torch.__version__}')"

Success Output: CUDA Available: True | Device: NVIDIA GeForce RTX 5090 | Version: ...dev2025...+cu130

Standard Installation (Non-5090 GPUs)

If you are NOT using an RTX 5090, you can use the standard installation method.

GPU Setup (RTX 30/40 Series):

# After base installation, install PyTorch with CUDA
uv pip install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu121

Check PyTorch installation guide for the appropriate CUDA version for your GPU.

Installation

Option 1: Using uv (Recommended)

Note: You don't need Python pre-installed! uv can install and manage Python for you.

1. Install uv (if not already installed):

   On Windows (PowerShell):

   powershell -ExecutionPolicy ByPass -c "irm https://astral.sh/uv/install.ps1 | iex"

   On macOS/Linux:

   curl -LsSf https://astral.sh/uv/install.sh | sh

2. Install Python 3.12.4 using uv (or any Python 3.9-3.12):

   uv python install 3.12.4

   Or install the latest Python 3.12:

   uv python install 3.12

   Note: AutoGluon 1.4.0 requires Python >=3.9,<3.13

3. Clone and navigate to the project:

   git clone <repository-url>
   cd mma-ai-db

4. Install dependencies (uv will automatically create a virtual environment):

   uv sync

   This command will:

   • Create a virtual environment automatically
   • Install all dependencies from pyproject.toml
   • Use the Python version managed by uv
5. Verify installation (optional):

   # Check AutoGluon installation
   uv run python -c "from autogluon.tabular import TabularPredictor; print('AutoGluon installed successfully!')"
   
   # Check GPU support (if applicable)
   uv run python -c "import torch; print('CUDA available:', torch.cuda.is_available())"

6. Run the application:

   uv run python main.py

   Or run tests:

   uv run pytest

Why This Works

The RTX 5090 uses NVIDIA's new Blackwell architecture, which requires CUDA 13 and the latest PyTorch Nightly builds. However, AutoGluon 1.4.0 was built and tested against older, stable PyTorch versions. By using --no-deps during AutoGluon installation, we bypass its dependency checks and manually install compatible versions of its sub-packages. This creates a working environment where PyTorch Nightly can communicate with your GPU while AutoGluon runs on top of it.

It's not elegant, but it works. And when you have a $2,000 GPU sitting in your machine, sometimes you need to get creative to make things work.

One of the hardest parts of training a sports model on UFC is the data drift. In 2016 the Vegas odds were only 61% accurate, then in 2024 they were something like 70% accurate. Right now we're seeing a small decline in the accuracy of Vegas. This is all just part of the ebb and flow of variance that also factors in general unpredictability of sports, especially UFC.

Critical implementation insights:

• Per-column effective n: Compute per-column n_eff and set weights to zero when that column has no opponent history, instead of COALESCE(..., 0) pretending it does.
• Global priors as safety net: Always have a global fallback row in weight-class prior CTEs so sparse classes never collapse toward zero.
• Per-stat K tuning: Tune K_mean vs K_mad per stat family. Generally K_mad > K_mean for stability with small samples.
• Time decay implementation: Use EXP(-λ * years_ago) with λ ≈ 0.13 for moderate decay over ~5 year half-life.

2) Poisson-Gamma Smoothing (Counts)

What was wrong before

• Under-specified exposure: I mixed count smoothing and rate logic inconsistently. The posterior mean was formed from (mean, variance) but I didn't consistently convert through exposure time when mapping back to counts. Short fights could look "low activity" for the wrong reason.
• Ad-hoc variance branch: When var ≤ mean I used a hand-rolled blend (e.g., (prior*3 + observed)/4). It stabilized things but it was a heuristic—not a model.
• One-size priors by year slice: Priors came from a fixed date window with mean/variance; no explicit rate per minute, and no principled pseudo-exposure strength.
• Binary/duration leakage risk: The old pass didn't clearly wall off duration (control time) or binary signals from count smoothing; at best they were excluded by name heuristics.

What I do now

• Rate-based Bayesian updating: I compute weight-class rates per minute (μ_w) and update with exposure time t (minutes). The posterior is λ_post = (μ_w * τ + X) / (τ + t), and I map back to counts via X_smooth = t * λ_post.
• Validated pseudo-minutes: τ (the prior strength) is per stat and sometimes per weight class (only when cross-validation showed ≥0.5% lift). Otherwise I fall back to global τ for consistency.
• Explicit exposure rules: Round-1 columns use min(time_sec_rd1, 300)/60; everything else uses time_sec/60. No more implicit exposure guessing.
• Strict scope: Count data only (e.g., *_land, *_att, kd, rev). Binary and duration stats are handled elsewhere.

Implementation Details for Your Own Model

Here's the specific SQL pattern I use for Poisson-Gamma smoothing:

-- Step 1: Compute weight-class rate priors
WITH wc_priors AS (
    SELECT weightclass,
           SUM(stat_count) / NULLIF(SUM(time_sec / 60.0), 0) AS wc_rate
    FROM fight_stats 
    WHERE time_sec > 0
    GROUP BY weightclass
),

-- Step 2: Apply Poisson-Gamma smoothing
smoothed AS (
    SELECT fight_id, fighter_id,
           -- Posterior rate: (prior_rate * pseudo_minutes + observed_count) / (pseudo_minutes + actual_minutes)
           (p.wc_rate * τ + fs.stat_count) / (τ + fs.time_sec / 60.0) AS posterior_rate,
           -- Convert back to smoothed count
           (fs.time_sec / 60.0) * 
           ((p.wc_rate * τ + fs.stat_count) / (τ + fs.time_sec / 60.0)) AS stat_count_smooth
    FROM fight_stats fs
    JOIN wc_priors p ON fs.weightclass = p.weightclass
)

-- Key insight: τ values I use:
-- Striking stats: τ = 15-25 minutes
-- Grappling stats: τ = 8-12 minutes  
-- Submission attempts: τ = 5-8 minutes

Critical implementation notes:

• Filter out zero exposure: Always add WHERE time_sec > 0 when computing priors to avoid division by zero.
• Round-1 exposure cap: For first-round stats, cap exposure at 300 seconds (5 minutes) since rounds can't exceed this.
• Pseudo-minute tuning: Start with τ=15 for most stats, then use cross-validation to optimize. Higher τ = more shrinkage toward prior.
• Weight-class fallbacks: Always have a global prior for weight classes with insufficient data.

Why this fixes the old issues

• Short/long fights handled correctly: A two-minute brawl vs. a fifteen-minute chess match are now comparable because smoothing happens on rates and returns properly scaled counts.
• Less hand-waving, more model: Pseudo-minutes encode prior confidence without ad-hoc branches; per-class overrides exist only where they earned their keep.

3) Beta-Binomial Smoothing (Binary)

What was wrong before

• There wasn't any. KO/Win/Decision/Sub were effectively raw indicators or simple ratios. That's noisy, mis-calibrated, and conflates "skill" with "opportunity."
• Attempts were undefined: I had no principled "denominator" for success probability. For example, calling every strike a KO attempt is just wrong.

What I do now

• Proper Beta-Binomial: For each binary family I define attempts and successes:
  • ko/win/decision: each fight is one opportunity.
  • sub_land: opportunities = sub_att.
  • ctrl (duration): modeled as a time-share (Bernoulli per second); smoothed rate times exposure seconds.
• Weight-class priors, validated strength: I use WC success rates as p priors and add pseudo-counts τ tuned per stat, optionally per WC where cross-validation justifies it (e.g., Featherweight subs, LHW/HW control).
• Zero-attempt guard: If attempts are zero, I return the WC/global prior rate rather than fabricating a fraction.

Implementation Details for Beta-Binomial Smoothing

Here's the exact approach for different binary outcomes:

-- For KO/Win/Decision rates (attempts = 1 per fight)
WITH wc_binary_priors AS (
    SELECT weightclass,
           SUM(CASE WHEN outcome = 'ko' THEN 1 ELSE 0 END)::float / COUNT(*) AS ko_rate,
           SUM(CASE WHEN outcome = 'win' THEN 1 ELSE 0 END)::float / COUNT(*) AS win_rate
    FROM fight_results
    GROUP BY weightclass
),

-- For submission success rates (attempts = sub_att, successes = sub_land)  
sub_priors AS (
    SELECT weightclass,
           SUM(sub_land)::float / NULLIF(SUM(sub_att), 0) AS sub_success_rate
    FROM fight_stats
    WHERE sub_att > 0
    GROUP BY weightclass
),

-- Apply Beta-Binomial smoothing
smoothed_binaries AS (
    SELECT fight_id, fighter_id,
           -- KO rate: (prior_rate * pseudo_attempts + successes) / (pseudo_attempts + attempts)
           (p.ko_rate * τ_ko + ko_success) / (τ_ko + 1) AS ko_prob_smooth,
           -- Sub rate: (prior_rate * pseudo_attempts + sub_land) / (pseudo_attempts + sub_att)  
           (sp.sub_success_rate * τ_sub + sub_land) / (τ_sub + GREATEST(sub_att, 1)) AS sub_prob_smooth
    FROM fight_stats fs
    JOIN wc_binary_priors p ON fs.weightclass = p.weightclass
    JOIN sub_priors sp ON fs.weightclass = sp.weightclass
)

-- Pseudo-attempt values I use:
-- KO/Win/Decision: τ = 8-12 fights
-- Submission success: τ = 3-5 attempts
-- Control time share: τ = 600-900 seconds

Key implementation considerations:

• Zero-attempt handling: When sub_att = 0, use the weight-class prior rate directly rather than trying to compute a ratio.
• Control time as time-share: Model control duration as Bernoulli per second, then multiply smoothed probability by total seconds.
• Minimum attempts: Use GREATEST(attempts, 1) to avoid division by zero in edge cases.
• Cross-validation tuning: Start with τ values above, then optimize per weight class only if CV shows >0.5% improvement.

Why this fixes the old issues

• Calibration: Probabilities stop over- or under-shooting because we borrow signal from the division realistically.
• Correct denominators: A sub success isn't "one per fight;" it's "out of sub attempts." A KO isn't "per strike;" it's "per fight." This matters.
• Principled uncertainty: Small sample sizes get more shrinkage, large samples trust their own data more.

4) Pipeline & Naming Hygiene

• Order matters: Binary smoothing runs before count smoothing (so sub attempts are raw counts when they need to be). After smoothing, I temporarily keep *_raw, compute derived stats (totals, accuracy, defense, ratios, per), then I drop *_raw. AdjPerf waits until opponent and weight-class aggregates are ready.
• Consistent feature families: Head/Body/Leg and Distance/Clinch/Ground share a naming pattern, so per/ratio/opp calculations can be reliably applied and diffed.

Why this fixes the old issues

• No accidental toggling: Derived features don't unknowingly mix raw and smoothed values.
• Less glue code, fewer footguns: Calculators can target families by suffix/prefix without bespoke filters for every one-off.

-- 1. Time decay weight calculation
SELECT EXP(-0.13 * EXTRACT(years FROM current_date - fight_date)) AS decay_weight

-- 2. Effective sample size (Kish formula)  
SELECT POWER(SUM(w), 2) / NULLIF(SUM(POWER(w, 2)), 0) AS n_effective

-- 3. Shrinkage toward prior
SELECT (n/(n + K) * observed + K/(n + K) * prior) AS shrunk_estimate

-- 4. Robust MAD calculation
WITH medians AS (
    SELECT PERCENTILE_CONT(0.5) WITHIN GROUP (ORDER BY stat_value) AS median_val
    FROM stats_table
),
deviations AS (
    SELECT ABS(stat_value - m.median_val) AS abs_dev
    FROM stats_table s CROSS JOIN medians m
)
SELECT PERCENTILE_CONT(0.5) WITHIN GROUP (ORDER BY abs_dev) AS mad_value
FROM deviations

-- 5. Exposure-corrected rate calculation
SELECT stat_count / GREATEST(time_minutes, 0.1) AS rate_per_minute

One of the hardest parts of training a sports model on UFC is the data drift. In 2016 the Vegas odds were only 61% accurate, then in 2024 they were something like 70% accurate. Right now we're seeing a small decline in the accuracy of Vegas. This is all just part of the ebb and flow of variance that also factors in general unpredictability of sports, especially UFC.

For the latest version of the model I spent a ton of time trying to really generalize the model so that I'm not overfitting to specific circumstances at any small point in time. These are the parameters I ended up settling on after hundreds of experiments:

train_size = 0.75     
val_size = 0.15        
test_size = 0.1 
n_splits = 4 
num_stack_levels = 2
use_recency_weights = True 
use_bag_holdout = True # Must be true if we're using tuning_data (val split)
num_bag_sets = 2
decay_rate = 0.13
shuffle = True
start_date = '2014-04-01'
calibrate = True

Breaking Down the AutoGluon Parameters

Let me explain each of these settings in simple terms:

• train_size/val_size/test_size: We use 75% for training, 15% for calibration validation, and 10% for final testing—larger validation than test because calibration requires substantial data to work properly.
• n_splits: Cross-fold validation uses 4 splits on the training data to ensure robust model selection.
• num_stack_levels: AutoGluon stacks models in 2 layers, where second-layer models learn from first-layer predictions.
• use_recency_weights: More recent fights are weighted heavier in training to capture current fighting trends.
• decay_rate: At 0.13, the earliest fight from 2014 weighs about 0.5 while the latest fight weighs about 1.5—making recent fights 3x more important.
• use_bag_holdout/num_bag_sets: Creates multiple model bags with holdout validation for better ensemble diversity.
• shuffle: Randomizes training order to prevent temporal bias during model training.
• calibrate: Applies post-hoc probability calibration to improve confidence score reliability.

For a long time I was doing a Cross-Fold Validation on 90% of the data, then the last 10% (about 1 year of the most recent fights) was left unseen as an impartial test of how well the model is generalizing to unseen future fights.

Cross-validation ensures robust model evaluation by training and testing on different data splits, helping prevent overfitting and providing more reliable performance estimates.

The Evolution of Validation Strategy

The reason for this was I wanted to maximize the most recent fight data to better predict near future results. As the years have gone by and I've gained a better overhead view of general variance in this sport, I'm slightly leaning towards really thinking through the architecture with generalization in mind will perform better over the long term rather than trying to maximize training data to the most recent fights. But like everything else in this journey, I'll experiment with this strategy and possibly revert back depending on how things go in the testing and real world as time goes on.

Once I started messing with calibration again I was required to go back to a train/val/test method where we do CFV on the train set then calibrate the predictions on val and get an unbiased evaluation of the model from unseen data on test.

So 2014-2023 is training, 2024 is calibration, and 2025 is test (more or less). Over hundreds of tweaks to the parameters above, this final set of parameters is showing the most consistency. I'm very sensitive to not just use the model that had the best results on the validation and test results because that can lead to overfitting where we just tuned parameters to maximize performance on the training and validation sets. Instead, we make sure that there isn't too much difference between validation and test set performance and that the training set performance isn't wildly higher than val/test. Results:

Training accuracy: 0.7511
Training log loss: -0.5082
Test accuracy: 0.7008
Test log loss: -0.5949
Val accuracy: 0.7072
Val log loss: -0.5918

Very nice sub -0.6 logloss and >70% accuracy on both the validation set and the unseen test set. Just to make sure we're not overfitting the model I started doing experiments where I use the same parameters and train the model based on cutoff dates, so how would these parameters perform if it didn't have access to the last 6 months of data or the last 12?

The P-Hacking Trap

Same parameters using data with a cutoff of 6 months ago:

Training accuracy: 0.7874
Training log loss: -0.4849
Test accuracy: 0.7149
Test log loss: -0.5785
Val accuracy: 0.6542
Val log loss: -0.6044

Reasonable. So I feel pretty good about the generalizability of the parameters I'm using right now and the training method implemented. I can p-hack the shit out of this though. For those unfamiliar, p-hacking is a term used in statistics where you "massage" the data or process so it looks like you're measuring some metric in a reasonable way but in fact you're just tweaking small portion of the stats so that the final benchmark metric like accuracy or logloss is maximized to make yourself look smart but isn't accurate to real-world measurement. For instance, what happens if I make a tiny change like increasing the initial data cutoff by 4 months from 2014-01-01 to 2014-04-01?

Training accuracy: 0.8460
Training log loss: -0.4122
Val accuracy: 0.7056
Val log loss: -0.5895
Test accuracy: 0.7121
Test log loss: -0.5864

Wowie weewah I improved the validation and test set logloss AND accuracy! I'm a motherfucking genius. This kind of improvement is unlikely to generalize to real world increases of accuracy and logloss. Look at the fact that the training accuracy increased by 6% leading to a larger gap between the training accuracy/logloss and the val/test logloss/accuracy. This is a negative improvement that likely means the model is a little bit more overfitted to the historical data.

You could argue this isn't that relevant since the unseen fight data accuracy and logloss improved and you wouldn't necessarily be wrong, but here in lies the difficulty of machine learning: you're always backtesting and there is no way to look into the future and tell how the model will actually perform in the real world, all you can do is decipher clues and the clue that stands out to me is a giant 6% leap in training data accuracy lead to an almost 15% gap between training accuracy and val/test accuracy. This is not good because we will never see 85% accuracy in unseen data, ever. We are straying further from Jesus with this minor change. We could've just eliminated a chunk of high variance fights where a bunch of unpredicted big underdogs won but by eliminating these high variance fights, we might've harmed the model's ability to recognize patterns in high variance fights that are still likely to occur in the future and so harmed the generalized ability of the model to predict future fights.

Why Not Include Odds as Features Anymore?

Because the odds accuracy vary wildly compared to more predictable sports like MLB, Soccer, or NFL. Again, the odds were 61% accurate in 2016 yet 70% accurate in 2024. Including the odds essentially makes the model subject to the whims of vegas rather than concretely generalizable over the long term. Second, since we have such highly engineered features, including the odds barely increases the accuracy of the model although it does improve the logloss quite well. All my odd-included models are -ROI on all down-the-line AI predictions because it so heavily favors betting the vegas odds favorite. It is useful still as a secondary measurement of risk-adjusted returns on favorites, but ultimately it's not that useful in generalized risk-adjusted returns on predictions.

Betting Strategy Performance Analysis

The real test of any model isn't just accuracy—it's profitability. Here's how different betting strategies performed over the latest backtest period, starting with $1,000 and betting $10 per pick:

Key Performance Metrics Explained

• ROI (%): Return on investment, measuring profit as a percentage of total amount wagered.
• Sharpe (ann.): Risk-adjusted return that accounts for volatility—higher values indicate better risk-adjusted performance.
• Sortino (ann.): Similar to Sharpe but only penalizes downside volatility, focusing on harmful risk.
• CAGR (%): Compound Annual Growth Rate, showing how fast your bankroll would grow annually.
• Max DD (%): Maximum drawdown, the largest peak-to-trough decline in bankroll value.
• Calmar: CAGR divided by maximum drawdown, measuring return per unit of downside risk.
• PF: Profit Factor, the ratio of gross profits to gross losses.
• ROI-Sharpe: A custom metric combining ROI and Sharpe ratio for overall strategy evaluation.

Model Calibration Analysis

Beyond profitability metrics, it's crucial to understand how well our AI model's confidence levels align with actual outcomes. A calibration curve shows whether the model's predicted probabilities match real-world frequencies—if the AI says a fighter has a 70% chance of winning, do they actually win about 70% of the time?

Calibration curve showing the relationship between predicted probabilities and actual outcomes. A perfectly calibrated model would follow the diagonal line—deviations indicate overconfidence (above line) or underconfidence (below line) in predictions.

The calibration curve reveals how reliable our model's confidence estimates are across different probability ranges. This is essential for betting strategies because misaligned confidence can lead to poor risk assessment—betting too heavily on picks the model is overconfident about, or missing value when the model is underconfident.

Key Insights from the Strategy Analysis

Lines generally move against us: The fact that the seven-day strategy consistently outperforms closing odds betting is a GREAT sign that the model is a sharp picker. When books adjust lines toward our picks by fight night, it validates our edge.

Risk-adjusted returns matter most: For gamblers, the most important metric isn't ROI, accuracy, logloss, or even expected value alone—it's risk-adjusted returns. You want sustainable profit without excessive volatility that can bankrupt you during inevitable losing streaks.

Based on the comprehensive analysis, the optimal strategy appears to be betting all AI picks within a 16% difference between the AI win probability and Vegas implied probability. For example, if the AI picks fighter1 at 70% and Vegas implied odds suggest 84%, we still bet on fighter1. Beyond this 16% threshold, we should consider placing half-unit bets AGAINST the fighter the AI picked.

Risk-Adjusted Strategy Performance

First, thanks to the community for helping me learn here (Shoutout to Jordan C. and the rest of you). To better understand the relationship between risk and reward across different betting strategies, we've analyzed the top 20 performing strategies based on their risk-adjusted returns. The scatter plot below shows each strategy's return on investment (ROI) versus its Sharpe ratio, which measures risk-adjusted performance.

Scatter plot showing ROI vs Sharpe ratio for the top 20 betting strategies. Strategies in the upper-right quadrant offer the best combination of high returns and good risk-adjusted performance.

The ideal strategies appear in the upper-right quadrant, offering both high ROI and strong risk-adjusted returns (high Sharpe ratio). This visualization helps identify strategies that not only generate profit but do so with manageable risk and volatility. Most of the "bet against AI pick based on (AI win% - Vegas odds implied probability) strategies have a cutoff of about 16-20%. Meaning the right time to bet against the AI profitably is when AI win% is at least 16-20% lower than the Vegas implied odds difference and even then it's probably not worth more than 1/2 a unit. The model appears to be very good at predicting underdogs at about a 50% rate, but it's general ability to accurately predict win% is still not as good as Vegas meaning betting solely on +EV isn't necessarily the best strategy.

Conclusion and Call for Feedback

Two important points:

1) Please be critical of this and send me unfiltered opinions and help. I have nowhere near the level of experience in picking betting strategies as I do in training models. The machine learning side I've got down, but translating statistical edges into optimal betting strategies is where I need the most improvement.

2) The data suggests our best approach is the nuanced edge-threshold strategy rather than blindly following all AI picks or only +EV selections. This makes intuitive sense—we trust the model most when it aligns reasonably well with market expectations, but we hedge when there's significant disagreement.

As always, this is an ongoing experiment. The beauty and curse of sports prediction is that the landscape constantly shifts. What works today might not work tomorrow, which is why building robust, generalizable systems matters more than chasing short-term optimization.

Get in Touch: The best place to reach me is on Patreon where the community shares free UFC predictions and discuss model development. You don't need to subscribe to participate in chats and direct messages—it's the most active community for discussing these predictions and sharing feedback. I'd love to hear your thoughts on the strategies and any suggestions for improvement!

Introduction

My UFC prediction model has maintained profitable performance for years despite having poorly calibrated probability estimates. While the model excels at binary classification (picking winners), its confidence scores don't align well with real-world win frequencies—a classic case of good accuracy, bad calibration.

This never bothered me much since the model was profitable, but I decided to experiment with post-hoc calibration methods to see if I could improve probability estimates without hurting classification performance. This post documents those experiments: the methods I tested, why most failed with limited data, and the modest improvements I eventually achieved with Platt scaling.

What is Model Calibration?

Model calibration refers to how well a model's predicted probabilities align with actual observed frequencies. A perfectly calibrated model should be correct 70% of the time when it predicts a 70% probability, 80% of the time when it predicts 80%, and so on.

Consider this example: if your model predicts 100 fights at 60% confidence, and the favored fighter wins 60 of those fights, your model is well-calibrated at that confidence level. However, if the favored fighter wins 75 times, your model is under-confident and poorly calibrated.

from sklearn.calibration import calibration_curve
import matplotlib.pyplot as plt

# Example: plotting calibration curve
fraction_pos, mean_pred = calibration_curve(y_true, y_prob, n_bins=10)
plt.plot([0, 1], [0, 1], 'k--', label='Perfect calibration')
plt.plot(mean_pred, fraction_pos, 's-', label='Model')
plt.xlabel('Mean Predicted Probability')
plt.ylabel('Fraction of Positives')

The Calibration vs. Accuracy Paradox

One of the most counterintuitive aspects of calibration is that improving probability estimates can sometimes hurt classification accuracy. This happens because calibration optimizes for probability-based metrics like log-loss and Brier score, while accuracy only cares about the binary decision boundary at 50%.

Why This Happens

Consider a model that consistently predicts 65% when the true probability is 60%. This model might achieve higher accuracy by being overconfident (correctly picking the winner more often due to increased confidence), but it's poorly calibrated. When calibrated, the model's predictions become more conservative, potentially crossing the 50% decision boundary in some cases and reducing accuracy.

In my UFC model, this manifested as:

Original Model Performance:
  Accuracy:    0.7098
  Log Loss:    0.6032
  Brier Score: 0.2075

Calibrated Model Performance:  
  Accuracy:    0.7098 (unchanged)
  Log Loss:    0.5979 (improved by 0.0053)
  Brier Score: 0.2056 (improved by 0.0019)

The accuracy remained stable while probability-based metrics improved significantly but that isn't true for all calibration methods and isn't even necessarily true 100% of the time for the method that actually worked.

The Small Sample Size Challenge

My dataset contains approximately 2,400 UFC fights over 10 years after extensive filtering:

def filter_fights(df, threshold, date='2015-01-01', include_split_dec=False):
    """
    Filter fights based on:
      - Binary results (y_true in [0, 1])
      - Both fighters must have had at least num_fights previous fights
      - Removing unwanted fight methods (DQ, split decisions, etc.)
      - Fights from 2015 onward
    """
    # Remove unwanted methods
    if include_split_dec:
        unwanted_methods = ['dq', 'other', 'overturned']
    else:
        unwanted_methods = ['dq', 'other', 'decision - split', 'decision - majority', 'overturned']
    
    # Filter to only binary results and recent fights
    df = df[df['y_true'].isin([0, 1])].copy()
    df = df[df['event_date'] >= pd.Timestamp(date)]
    
    return df

This small sample size created significant challenges for calibration, particularly with isotonic regression which requires sufficient data points across the probability spectrum.

Isotonic Regression: The First Attempt

Isotonic regression is a non-parametric calibration method that learns a monotonic mapping from predicted probabilities to calibrated probabilities. It's theoretically superior to Platt scaling as it can capture non-linear calibration relationships.

class SimpleIsotonicCalibration:
    def __init__(self, y_min=0.01, y_max=0.99):
        self.y_min = y_min
        self.y_max = y_max
        self.calibrator = None
        
    def fit(self, y_prob, y_true):
        from sklearn.isotonic import IsotonicRegression
        
        self.calibrator = IsotonicRegression(
            y_min=self.y_min,
            y_max=self.y_max,
            out_of_bounds='clip'
        )
        self.calibrator.fit(y_prob, y_true)

Isotonic Results (Disappointing)

Isotonic Calibration Results:
Should Use Calibration: False
Calibration Set Log Loss Improvement: 0.0553 # Improvement on the calibration set of data
Test Set Log Loss Improvement: 0.0125  # Worse on the unseen test set!
Test Set Brier Score Improvement: 0.0023 # Worse on the unseen test set!
Final Test Log Loss (Original): 0.5937
Final Test Log Loss (Calibrated): 0.6063

The isotonic calibration actually hurt performance on the test set despite improving calibration set metrics. This is a classic sign of overfitting due to insufficient data.

Why Isotonic Failed

1. Small sample size: With only ~240 test samples (10% of 2,400), isotonic regression had insufficient data to learn a robust monotonic mapping
2. Sparse probability regions: Some probability ranges had very few examples, leading to unreliable calibration
3. Overfitting: The flexibility of isotonic regression became a liability with limited data

I attempted several improvements:

• Ensemble approach: Multiple isotonic regressors trained on different CV folds using all the training data. This was dumb because I was just training the calibration model on fights the main model had already been trained on leading to overfitting on train, and poor results on the holdout test dataset.
• Expanded calibration set: Increased from 10% to 20% of data
• Parameter tuning: Adjusted y_min, y_max, and out_of_bounds settings

None of these approaches yielded meaningful improvements.

Platt Scaling: A Little Better

Platt scaling uses logistic regression to map uncalibrated probabilities to calibrated ones. While less flexible than isotonic regression, it's much more suitable for small datasets.

class SimplePlattCalibration:
    def __init__(self, max_iter=100, random_state=42):
        self.max_iter = max_iter
        self.random_state = random_state
        self.calibrator = None
        
    def fit(self, y_prob, y_true):
        from sklearn.linear_model import LogisticRegression
        
        # Reshape probabilities for sklearn (needs 2D input)
        y_prob_reshaped = y_prob.reshape(-1, 1)
        
        self.calibrator = LogisticRegression(
            max_iter=self.max_iter,
            random_state=self.random_state,
            solver='lbfgs'
        )
        self.calibrator.fit(y_prob_reshaped, y_true)

Implementation in Training Pipeline

The calibration was integrated into the training pipeline using scikit-learn's CalibratedClassifierCV:

# Three-way split for proper calibration validation
(X_train, y_train), (X_cal, y_cal), (X_test, y_test) = split_data_three_way(
    X, y, train_size=0.775, val_size=0.125
)

# Wrap AutoGluon predictor for sklearn compatibility
autogluon_wrapper = AutoGluonWrapper(predictor, feature_columns=X_train.columns.tolist())

# Create calibrated classifier using holdout method
calibrated_clf = CalibratedClassifierCV(
    estimator=autogluon_wrapper,
    method='sigmoid',  # Platt scaling
    cv="prefit",       # Use prefit since AutoGluon is already trained
    ensemble=False     # Use single calibrator since we have proper split
)

# Fit calibrator on holdout calibration set
calibrated_clf.fit(X_cal_clean, y_cal)

Platt Scaling Results (Success!)

Calibration Results (sigmoid):
Should Use Calibration: True
Calibration Set Log Loss Improvement: 0.0098
Test Set Log Loss Improvement: 0.0107
Test Set Brier Score Improvement: 0.0043
Test Set ECE Improvement: 0.0174
Final Test Log Loss (Original): 0.5948
Final Test Log Loss (Calibrated): 0.5841

The improvement of 0.0107 in log-loss on the holdout test set of data represents a meaningful, if small, gain in probability accuracy.

Profitability Impact Analysis

While the statistical improvements were modest, I wanted to examine whether calibration affected betting profitability. Here's the cumulative profit comparison between the original and calibrated models on the test set:

The results show modest but consistent improvements across most betting strategies. The core strategy (ai_all_picks_closing) improved from 13.26% to 13.60% ROI, while the seven-day advance strategy increased from 14.98% to 15.30% ROI. Notably, win percentages remained identical at 70.70% which is interesting because some picks do change based on the calibration process.

Interestingly, underdog-focused strategies saw slight decreases in ROI (35.31% to 34.97% for closing odds) and slightly improved favorite win percentages (70.70% to 70.80%), suggesting the calibration process may have made the model slightly more conservative on high-value underdog picks. Meanwhile, the poorly performing +EV on ANY fighter (regardless of AI pick) strategies remained unprofitable in both versions but dramatically improved in the calibrated version showing the calibration process working in action. The AI-picked +EV strategy was basically the same though which tells me I need more profit testing on where the +EV threshold is, like +5% win chance? +10% win chance? When do we bet against the AI pick? Like last event Kevin Holland was picked by AI at -180 or something yet Vegas had him at -500. What's the threshold to pick against the AI? IDK yet but I'll go test it out. This is the most pressing question when we're talking about betting strategy.

However, it's crucial to note that ROI is a moving target—betting markets evolve, line movement varies, and small sample sizes can significantly impact results. These profit tests represent performance on a specific test set and shouldn't be viewed as guaranteed future returns. The real value of calibration lies in more reliable probability estimates for bet sizing and strategy decisions rather than raw profit maximization.

Model Performance Analysis

Here's how the calibrated model performed against Vegas odds across all unfiltered fights in the past 1.5 years (meaning we include split decisions, and DQ's, and whatnot which aren't included in the model training):

{
  "vegas_odds_performance": {
    "accuracy": 0.700,
    "log_loss": 0.563,
    "brier_score": 0.194
  },
  "mma_ai_performance": {
    "accuracy": 0.710,
    "log_loss": 0.603,
    "brier_score": 0.208
  },
  "mma_ai_performance_calibrated": {
    "accuracy": 0.710,
    "log_loss": 0.598,  # Improved
    "brier_score": 0.206  # Improved
  }
}

The calibrated model maintains identical accuracy while providing more reliable probability estimates.

The Calibration Curve Analysis

The most telling evidence comes from the calibration curve itself. My uncalibrated model exhibited classic miscalibration patterns:

• Underconfident in 50-60% range: When the model predicted 55%, fighters actually won ~60% of the time
• Overconfident in 40-50% range: When the model predicted 45%, fighters won closer to 40% of the time

def plot_calibration_curve(self, n_bins=10, include_all_fights: bool = False):
    # Get calibrated predictions if calibrator is available
    y_prob_calibrated = None
    if self.calibrator is not None:
        y_prob_calibrated = self.calibrator.predict_proba(test_data_clean)[:, 1]
    
    # Calculate calibration curves
    prob_true_model, prob_pred_model = calibration_curve(self.y_test, y_prob_model, n_bins=n_bins)
    if y_prob_calibrated is not None:
        prob_true_calibrated, prob_pred_calibrated = calibration_curve(
            self.y_test, y_prob_calibrated, n_bins=n_bins
        )
    
    # Plot results
    plt.plot([0, 1], [0, 1], 'k--', label='Perfect Calibration')
    plt.plot(prob_pred_model, prob_true_model, 's-', label='Model (Original)')
    if y_prob_calibrated is not None:
        plt.plot(prob_pred_calibrated, prob_true_calibrated, '^-', 
                label='Model Calibrated', alpha=0.8)

The Odds Inclusion Paradox

An interesting discovery was the relationship between including betting odds and calibration. In previous experiments 1-2 years ago, calibration consistently hurt performance. The key difference was I was including Vegas odds as features.

With Odds (Historical)

• Pros: Exceptional calibration, higher accuracy (~73-74%)
• Cons: Model HEAVILY favored odds over other features, struggled with underdog picks, -6% lower ROI against all model picks

Without Odds (Current)

• Pros: Better underdog detection, higher betting ROI, room for calibration improvement
• Cons: Lower accuracy (~71%), requires manual calibration

This represents a fascinating tradeoff: accuracy vs. profitability. The model without odds hits significantly more profitable underdog picks, even though its raw accuracy is lower.

Why Calibration Matters for Bettors

While calibration may not be necessary for a profitable model (mine was already profitable before calibration), it provides crucial benefits for bet sizing and strategy:

Kelly Criterion Application

With well-calibrated probabilities, bettors can use the Kelly Criterion more effectively:

def kelly_bet_size(prob, odds, bankroll):
    """Calculate optimal bet size using Kelly Criterion"""
    decimal_odds = american_to_decimal(odds)
    edge = prob * decimal_odds - 1
    if edge <= 0:
        return 0
    kelly_fraction = edge / (decimal_odds - 1)
    return min(kelly_fraction * bankroll, bankroll * 0.1)  # Cap at 10%

I experimented with fractional kelly in the past. It's promising long term, especially since the model's logloss is consistently less than .059, but the wild swings are too painful. If we got the model to be lower logloss than Vegas by including the odds in the feature set I think this is promising but will experiment more later with that.

Confidence-Based Strategies

Calibrated probabilities enable more sophisticated betting strategies:

def edge_based_betting_strategy(predictions, min_edge=0.05):
    """Select bets based on edge over Vegas odds rather than absolute confidence."""
    betting_opportunities = []
    
    for fight in predictions:
        # Get model probability and Vegas implied probability
        model_prob = fight['model_confidence']
        vegas_decimal_odds = american_to_decimal(fight['vegas_odds'])
        vegas_implied_prob = 1 / vegas_decimal_odds
        
        # Calculate edge (model probability - market probability)
        edge = model_prob - vegas_implied_prob
        
        # Only bet if we have a significant edge
        if edge >= min_edge:
            kelly_fraction = edge / (vegas_decimal_odds - 1)  # Kelly criterion
            betting_opportunities.append({
                'pick': fight['fighter_name'],
                'edge': edge,
            })
    
    return betting_opportunities

I'll probably implement something like this later on after I do more profitability backtesting with flat units.

Technical Implementation Details

The final calibration system integrates seamlessly with the existing prediction pipeline:

def _get_model_predictions(self, test_data, use_calibrated=None):
    """Get model predictions, optionally using calibrator."""
    if use_calibrated is None:
        use_calibrated = self.calibrator is not None
    
    # Get original predictions
    y_pred = self.predictor.predict(test_data)
    y_prob = self.predictor.predict_proba(test_data)
    
    # Apply calibration if available
    if use_calibrated and self.calibrator is not None:
        test_data_clean = test_data.drop(columns=['sample_weight'], errors='ignore')
        y_prob = self.calibrator.predict_proba(test_data_clean)[:, 1]
        y_pred = (y_prob > 0.5).astype(int)
    
    return y_pred, y_prob

Lessons Learned

1. Dataset size matters: Isotonic regression requires substantial data; Platt scaling works better with limited samples
2. Validation strategy is crucial: Proper train/calibration/test splits prevent overfitting
3. Calibration ≠ Accuracy: Better probabilities don't always mean better classifications
4. Feature engineering impacts calibration: Including odds improves calibration but hurts profitability
5. Domain expertise guides tradeoffs: Understanding the betting market informed the decision to exclude odds

Conclusion

While the final improvement in logloss was modest (0.0107), it represents a meaningful step toward more reliable probability estimates.

The key insight is that calibration serves different purposes depending on your goals. For pure classification accuracy, it is unnecessary. For models that are already well calibrated (like when you include the odds, or use algos that are better for calibration like Random Forest) calibrating the predictions using Platt or Isotonic harms the output.

The surprising relationship between feature inclusion (odds) and calibration highlights the complex tradeoffs in machine learning systems. Sometimes the most accurate model isn't the most profitable one, and the most calibrated model isn't the most accurate one.

For practitioners working with limited datasets, Platt scaling offers a robust path to improved calibration. The simplicity of logistic regression makes it both interpretable and reliable, even when more sophisticated methods fail.

Not at this time. I've spent so many hours investigating this in my free time. ROI is our north star, with logloss and accuracy being secondary metrics. This isn't a perfect test because the betting markets shift as time moves. For example, 2016 saw Vegas favorites win only 61% of the time. 2024 saw favorites win 70% of the time and UFC red corner is usually the betting odds favorite. So this isn't the end-all be-all conclusion, but it is absolutely the point in time conclusion.

The long and short of the massive amount of trial and error is this backtested ROI based on the last year of fights the model has never seen:

ROI Comparison: Balanced vs Unbalanced Training

ROI of balanced 50/50 fighter1 win/lose:

ROI of unbalanced 59/41 fighter1 (UFC assigned red corner) win/lose:

Based on how I do feature engineering and model tuning, balancing the fighters' win rate before training the model is terrible. If I do some various feature and model tuning I can see the balanced model start to perform closer to the unbalanced model but on average it is basically always lower ROI. I have interrogated my code a thousand times with Claude4 Opus and Gemini 2.5 Pro to try to suss out any logical errors and I cannot find any.

Why Does Balanced Training Destroy Performance?

*Begin speculation*

Distribution shift between training and inference creates systematic probability miscalibration. When you balance the dataset to 50/50, you're teaching the model that P(fighter1_wins) = 0.5 across all feature combinations. But in reality, fighter1 (red corner) wins ~60% of the time because the UFC systematically assigns the red corner to champions in title fights and generally more experienced/favored fighters in regular bouts.

The calibration mismatch:

• Training: Model learns P(fighter1_wins | features) where the base rate is artificially 0.5
• Inference: Model predicts on data where the true base rate is 0.6

This specifically destroys betting ROI because:

• Systematic underestimation of favorites: When a red corner fighter should win with 70% probability, your balanced model might predict 60%, causing you to miss profitable favorite bets
• Systematic overestimation of underdogs: When a blue corner fighter should win with 30% probability, your model might predict 40%, leading to negative EV underdog bets
• Market inefficiency amplification: The higher ROI without balancing implies that the model is learning this pattern of corner bias more efficiently than the market is.

The model's probability outputs are fundamentally miscalibrated for the real world's corner assignment bias. You're essentially training a model for a balanced fantasy UFC and then applying it to the systematically biased real UFC, where corner assignments carry predictive information about fight outcomes.

Bottom line: The balanced training throws away valuable signal (red corner = usually stronger fighter) and teaches the model incorrect base rates, leading to systematically poor probability estimates that destroy betting performance.

Doesn't Calibrating the Winrate Just Create a Proxy for the Odds?

No, and here's why that concern misses the point:

The model isn't learning "red corner = bet favorite." It's learning complex feature interactions from granular performance statistics that happen to correlate with corner assignments. The red corner correlation exists because the UFC assigns corners based on ranking, championship status, and experience - the same underlying factors that drive fight outcomes.

Key distinctions:

• Betting odds reflect public perception, line movement, and bookmaker risk management
• The model analyzes actual performance metrics: strike accuracy trends, takedown defense patterns, cardio indicators, opponent-adjusted statistics, etc.
• The value comes from divergence identification based on as much statistical information as possible. The corner bias is simply real world information that the model can learn to incorporate better than average bettors.

The unbalanced training preserves the signal that corner assignments carry meaningful information about fighter quality, information that's already baked into the real-world problem you're trying to solve. Throwing away that signal artificially handicaps the model's ability to make properly calibrated predictions.

What About Including the Odds?

This is a hotly debated topic in the sports betting community. Bill Benter, one of the fathers of algo betting, argued that the odds are best to be included because they encode so much information. Having been testing this hypothesis for many thousands of hours, my conclusion is that if you don't have a certain level of extremely high quality engineered features, then yes you should include the odds. But at a certain point, the features you engineers will actually encode more information in combination than the odds do. At that point, including the odds simply lowers the ROI.

Mathematical Mechanism

When you include odds as a feature, you're introducing a variable that represents the market's aggregated probability estimate: P_market(fighter1_wins). This creates several mathematical problems:

1. Feature Dominance and Prediction Convergence
Tree-based models will heavily weight the odds feature because it exhibits high mutual information with the target across the entire dataset. The model's predicted probabilities become:

P_model(fighter1_wins) ≈ α·P_market + (1-α)·P_stats where α > 0.5

This forces convergence toward market consensus.

2. Outcome Distribution Skew
Including odds biases the model toward predicting high-frequency, low-profit outcomes (favorites). Your engineered statistics without odds bias toward identifying low-frequency, high-profit outcomes (underdog value).

3. +EV Prediction Accuracy Inversion
The critical insight: ROI optimization requires accuracy specifically on profitable bets, not overall accuracy.

• With odds included: Model achieves ~74% accuracy but concentrates correct predictions on favorites (odds = 1.2-1.8, profit margin = 20-80%)
• Without odds included: Model achieves ~71% accuracy but concentrates correct predictions on underdogs (odds = 2.5-4.0, profit margin = 150-300%)

ROI Mathematics

Consider two hypothetical models:

• Model A: 75% accuracy, predicts favorites 85% of the time → Expected ROI ≈ -2% (high accuracy, low margins, vig erosion)
• Model B: 50% accuracy, predicts underdogs 60% of the time → Expected ROI ≈ +15% (lower accuracy, exponentially higher margins)

The fundamental equation:

ROI = Σ(accuracy_i × frequency_i × profit_margin_i)

Your empirical results demonstrate that excluding odds increases accuracy_underdog dramatically while slightly decreasing accuracy_overall. Since profit_margin_underdog >> profit_margin_favorite, the ROI optimization occurs through maximizing performance on the subset of predictions with the highest profit potential.

Information Compression Loss

Odds represent market consensus based on public information flow. Your engineered features capture orthogonal signals that specifically identify cases where statistical analysis diverges from public perception—exactly the scenarios that generate +EV opportunities. Including odds suppresses these divergent signals in favor of consensus alignment, destroying the edge that creates profitable betting opportunities.

The Vanity Metrics Problem in Machine Learning

You will see many other novice machine learning engineers practice their skills against sports prediction. They will calibrate their models against vanity metrics like accuracy in most cases. They will see evaluations like 85% accuracy, then not have any motivation to figure out why their model will fail in the real world then make a YouTube or Medium post about it.

This represents the fundamental disconnect between academic machine learning and profitable real-world application. The sports prediction space is littered with impressive-sounding accuracy claims that evaporate when subjected to actual betting markets. These engineers optimize for metrics that sound impressive in blog posts rather than metrics that generate alpha.

The vanity metrics obsession creates a particularly insidious blind spot: data leakage and overfitting become invisible when you're chasing high accuracy numbers. Consider the classic example in YouTube tutorials (https://www.youtube.com/watch?v=LkJpNLIaeVk) where a model achieved impressive accuracy predicting UFC fights using Elo ratings... except they used post-fight Elo ratings for training, meaning the model literally saw fight outcomes during training. This is textbook data leakage: using future information to predict past events.

Data Leakage Examples in Sports Prediction:

• Training on post-game statistics to predict game outcomes
• Including betting line movements that occurred after the event
• Using season-end rankings to predict mid-season games
• Including opponent-adjusted metrics calculated after the fight

The overfitting trap compounds this problem. Hyperparameters are the configuration settings that control how a model learns: things like learning rate, tree depth, regularization strength. I can easily tune these hyperparameters to achieve 78% accuracy on my validation set by optimizing for that specific data slice. But this creates a model that memorizes the validation set's quirks rather than learning generalizable patterns.

The feedback loop is broken: High accuracy on test data → immediate gratification → publish results → never discover real-world failure. There's no motivation to dig deeper because the vanity metric has been satisfied. The engineer never learns that their 85% accuracy model would lose money consistently because they never actually test it against betting markets.

Real-World Adversarial Markets

Real-world sports betting is an adversarial market where you're competing against:

• Professional odds compilers with decades of experience
• Sophisticated betting syndicates with proprietary data
• Market makers who adjust lines in real-time based on money flow
• The inherent vig that makes break-even betting a losing proposition

Simply achieving high accuracy on historical data means nothing if your predictions can't consistently identify mispriced markets. The difference between academic exercise and profitable application is the difference between predicting outcomes and finding edges.

Lessons from Four Years of Iteration

I'm four years into this space and I've made all the same mistakes. I've built models that achieved 78% accuracy and lost money consistently. I've spent months optimizing for log loss improvements that translated to worse ROI. I've fallen into every trap outlined above because the feedback loop between model performance and real-world profitability is opaque until you actually start tracking betting results over extended periods.

This is a far more complex problem than I ever initially thought 4 years ago, but I believe what's outlined above is one of the reasons I've been seeing almost 20% ROI over the past few years in my free, public predictions. The key insights around dataset balancing, odds inclusion, and ROI-focused optimization came from years of iterative failure and debugging, not from following standard ML tutorials.

The engineering rigor required to build profitable models demands treating accuracy as a vanity metric and ROI as the only metric that matters with the knowledge that betting markets shift as time goes on and you must constantly retrain the model to match the current zeitgeist. Hence why I'm on version 6.3 right now. I've redone 100% of the code 6 times now. If you want to avoid the same mistakes I've made, feel free to reach out. I'm an open book on exactly how I built this model, no secrets. And also, as usual, shoutout to Chris from Wolftickets.ai for being one of the very very few people in this ML for sports prediction field that actually shared his technical knowledge and saved me endless hours of wasting my time. I like paying that forward to others who are interested in this space.

I have released v6.1 of the model. Large improvement in accuracy but most specifically in ROI. So let's talk betting strategy. One question I get asked practically every day is, "why do you recommend only the AI picked winners even if they're not +EV?"

The best tech available for predicting UFC are binary classification algorithms. These are algorithms specialized in classifying a fighter as either 1 or 0, win or loss. The confidence score that the algorithm comes up with is not its fundamental strength.

"So why don't you calibrate it?"

Because the calibration tech we have for these algorithms suck. Platt Scaling and Isotonic Regression are the two most potent weapons we have to calibrate these predictions. I have experimented a lot with them. 100% of the time they suck. They lower the accuracy and the ROI. I've experimented with custom calibrations but it's just too inconsistent and I don't see a promising way forward. I would absolutely love to have better calibration, so if you have any ideas please let me know. That being said, the ultimate goal here is risk-adjusted returns. Calibration is a tool to help us get there but it's not necessary to acheiving the goal.

Anyway, who cares about calibration if we're making fat ROI? Take off your sports bettor hat and all the "fundamentals" you know like +EV is all that matters to be successful. Put on your machine learning cap and look at the data. This is the calibration curve:

Note how the model is highly underconfident in its 50-65% confidence score picks and highly overconfident in it's 35-50% confidence scores. The nature of the algorithm is to maximize it's ability to successfully pick the winner and it does this at the expense of accurate calibration. It clusters it's confidence scores in the 50-65% range. AND THAT'S OK!

Here's the model evaluations and vegas evaluations on the last year of unseen fights:

Note the model is more accurate than Vegas, but it's logloss and Brier scores (essentially real world win%) are worse. Again, THIS IS OK. Why? Because look at these profit strategy backtests over the last year of unseen fights:

The fundamental strategy of betting on 100% of the AI picks on the closing odds is 14% profitable (ai_all_picks_closing). The strategy of picking only the +EV fighter based on the AI confidence score whether the AI picked that fighter to win or not is -0.5% unprofitable (any_fighter_positive_ev_closing).

Interpreting The Strategies

None of this is to say that +EV isn't a helpful metric. Look at another fundamental strategy, betting only on +EV AI-picked fighters (ai_picked_positive_ev_closing): +24.2% ROI. 10% higher than just doing down the line bets but it means sometimes there'll be events where you don't get to bet which makes me sad.

So let's put this all together. Why are parlays so good with this machine learning algorithm? It's because the algorithm is so gosh darn good at picking winners. Parlaying the AI picks, whether +EV or not, is a highly profitable strategy. The best strategy is doing 2 to 3 leg parlays on the +EV AI picked fighters. I'll probably move into posting these parlays again in the homepage.

EDIT: Shoutout to @Heisenb3rg on X for bringing Sharpe Ratios to my attention! This is a crucial metric from finance that measures risk-adjusted returns. Essentially, it tells us how much return we're getting for the amount of risk (volatility) we're taking on with a particular betting strategy. A higher Sharpe Ratio is better.

Looking at the Sharpe Ratio analysis, we can see how different strategies compare not just on raw ROI, but also on how bumpy the ride is. For v6.1, the 'ai_picked_positive_ev_closing' strategy seems to offer a strong balance, providing good returns without excessive risk compared to some others. However, the 'ai_all_picks_closing' still performs well from a risk-adjusted perspective, offering broader betting opportunities.

So, what's the takeaway? While different model versions might favor underdogs or favorites differently, the data consistently points towards a simple, robust approach. Considering both the ROI and the Sharpe Ratio (risk-adjusted return), the strategy of betting on all AI picks using the odds available 7 days before the event (ai_all_picks_7day) emerges as the winner. It offers the best blend of profitability and lower volatility, making it the simplest and most effective core strategy based on the current analysis.

It's important to remember that model performance, especially regarding favorites versus underdogs, can shift between versions and timelines. Therefore, relying solely on specific odds ranges like underdogs only might be less reliable long-term despite being very profitable over the past year. Instead, I think focusing on fundamental strategies evaluated through metrics like ROI and Sharpe Ratio is key. For the current model, based on the patterns I've seen over the years, I think I'm going to stick with the core strategy ai_all_picks_sevenday which provides the best risk-adjusted performance indicated by the Sharpe Ratio. To get higher returns at higher risk, 2 to 3 leg parlays of your choice are a good option.

Here are the AI predictions for UFC 314.

Check out the latest video analysis and AI predictions for the upcoming UFC matchup between Emmett and Murphy. The AI generated interpretation of my face always cracks me up.

Check out our latest video explaining how MMA-AI makes its predictions and why our model has been consistently outperforming Vegas odds.

After countless requests from the community, I'm finally pulling back the curtain on how our UFC fight prediction algorithm works. This isn't just another black-box system—it's a carefully engineered, multi-level approach to fight analysis that's consistently outperforming Vegas odds.

Why Share Our Secret Sauce?

Many have asked why I'd reveal the inner workings of a profitable system. The truth is simple: I don't believe in keeping this knowledge secret. Much of this algorithm was developed with the assistance of AI tools that generated about 90% of my code. As someone who's been an open source developer for 15 years, I firmly believe that open knowledge sharing accelerates human progress. I don't have a moat to protect—and frankly, the more people who understand these concepts, the faster our collective knowledge will advance. Sports prediction is hard enough that even with this blueprint, you'll still need to invest thousands of hours to truly master it.

The Four Levels of Fight Prediction

Level 1: Foundation Stats + Bayesian Gamma-Poisson Smoothing

We start with raw fight statistics—strikes thrown, takedowns landed, control time, and dozens more. But raw numbers can be misleading, especially for rare events like submissions. This is where Bayesian Gamma-Poisson smoothing comes in.

Imagine a fighter who's attempted only one submission in their career and landed it. Is their submission accuracy really 100%? Probably not. Gamma-Poisson smoothing helps us balance observed data with prior knowledge, preventing outliers from skewing predictions. For high-volume stats like significant strikes, the smoothing effect is minimal. But for rare events like submissions or knockdowns, it provides crucial stability by "pulling" extreme values toward more realistic expectations based on the fighter's division and overall UFC averages.

Level 2: Comparative Analysis

Next, we calculate a fighter's efficiency metrics: accuracy (how often attacks land), defense (how often they avoid opponents' attacks), output per minute, and the ratios between fighters across all statistics. This gives us a clearer picture of how fighters perform relative to each other, beyond just counting actions. A fighter might land fewer strikes overall but have significantly higher accuracy—a crucial distinction our model captures.

Level 3: Time-Weighted Averages + Variability

MMA evolves rapidly, and a fighter today isn't the same as they were three years ago. We calculate both standard and time-decayed averages with a 1.5-year half-life for all statistics. This means a fight from three months ago has far more impact on our predictions than one from three years ago.

Additionally, we measure the variability of these stats using Median Absolute Deviation (MAD) instead of standard deviation. MAD is less affected by extreme outliers, providing a more stable measure of how consistent a fighter's performance has been.

Level 4: Adjusted Performance (AdjPerf)

Our most sophisticated metric answers a critical question: how does a fighter perform against a specific opponent compared to how that opponent's previous adversaries performed? This z-score normalization looks like:

stat_adjperf = (fighter1_stat - fighter2_stat_prev_opp_avg) / fighter2_stat_prev_opp_mad

In plain English: we're measuring how much better or worse a fighter performed against their opponent compared to what we'd expect based on the opponent's history. If a fighter lands more strikes against someone who's historically difficult to hit, that's far more impressive than landing the same number against someone who's easily hit. AdjPerf captures this crucial context.

Building the Prediction Model

With thousands of engineered features from these four levels, we use Autogluon (thanks to Chris from Wolftickets.ai for this recommendation) to train our prediction model. Using presets like "experimental" and time-ordered data splitting (typically 80/20 or 90/10 train/test), we run extensive cross-validation to ensure reliability.

There's no definitive guide to sports prediction—we've conducted thousands of hours of testing to find what consistently beats Vegas odds. Everything from feature selection to hyperparameter tuning requires constant experimentation and refinement. What works for NFL might not work for UFC, and what worked last year might not work next year.

The final model combines about the 30 best of these features, weighted according to their predictive power. The result is a system that consistently identifies value bets where our predicted win probability exceeds what Vegas odds imply.

The Practical Limitations of ML Probabilities

One of the humbling lessons I've learned over the years is about the relationship between machine learning and betting strategy. Despite the sophisticated nature of our model, I've had to accept that ML algorithms have inherent limitations when it comes to probability calibration. While traditional betting approaches rely heavily on expected value (EV) calculations, I've discovered that applying these same principles directly to ML outputs can be problematic. Our tabular ML models excel at binary classification—essentially determining which fighter is more likely to win—but their confidence scores aren't necessarily true probabilities in the statistical sense. Even when optimizing for log loss (which theoretically improves probability calibration), there remain subtle biases and distortions in how these models estimate probabilities. Through trial and error, I've found that treating the model's outputs as relative confidence levels rather than exact win probabilities leads to more consistent results. Instead of rigidly applying EV formulas, we use confidence thresholds as a filtering mechanism to identify promising bets. This pragmatic approach acknowledges the model's strengths in pattern recognition while respecting its limitations in precise probability estimation—a balance that has proven more effective than assuming perfect calibration.

Visualization of our model's prediction distribution compared to actual outcomes, showing the effectiveness of our approach despite calibration challenges.

Why Current LLM-Based Fight Predictions Fall Short

I've extensively tested Large Language Models (LLMs) like GPT-4 for fight predictions, and the results have been consistently disappointing. The fundamental limitation is clear: today's LLMs lack the ability to analyze fight footage. They're trained primarily on text data, which means they miss crucial visual information—a fighter's movement patterns, subtle defensive vulnerabilities, changes in stance, or signs of fatigue that only appear on video. Statistical data can tell us a lot, but the visual dimension of fighting contains irreplaceable insights that no spreadsheet can capture. The good news? This limitation is temporary. Within the next 1-2 years, we'll see multimodal AI systems trained on vast libraries of video footage, capable of analyzing thousands of fights frame-by-frame. When that happens, AI fight prediction will undergo a revolutionary leap forward. Until then, the most effective approach remains combining sophisticated statistical modeling with human expertise for context and interpretation.

Conclusion: The Never-Ending Journey

MMA prediction remains as much art as science. While our technical approach provides an edge, the sport constantly evolves, and so must our model. Every event brings new data, every fighter brings new patterns, and our system continually adapts to these changes.

Whether you're a casual fan or a serious bettor, I hope this behind-the-scenes look helps you appreciate the depth of analysis that goes into each prediction you see on MMA-AI.net. And if you're inspired to build your own model? Even better—innovation thrives when knowledge is shared.

Model v6 is available for tonight's event and events going forward. This is intended to be a long-term release.

Changes:

• Unit tests for everything
  • Finally we have unit tests for all calculations so I can sleep at night. At least now if the model fails I know it's not some unknown bug.
• Bayesian Gamma-Poisson
  • We switched out from just doing Bayesian Beta Binomial smoothing in accuracy/def and per_min calculations to a Bayesian Gamma-Poisson for all stats starting at the very beginning. This is a more robust and consistent smoothing factor.
• Swapped stddev for median absolute deviation for the zscore normalization stat adjperf
  • Adjperf layer of feature engineering changed from:
    stat_adjperf = (fighter1_stat - fighter2_stat_prev_opponents_avg) / fighter2_stat_prev_opponents_stddev
    to:
    stat_adjperf = (fighter1_stat - fighter2_stat_prev_opponents_avg) / fighter2_stat_prev_opponents_mad
  • Median absolute deviation (MAD) is a more robust measure of deviation for sports statistics because it's not as vulnerable to outliers.

Future:

Have a few stats I'd still like to engineer especially around the win conditions of submissions vs KO vs decision.

I have also added visualizations to the predictions. Just hover over the fight or click on the fight to see how each fighter compares to each other using a normalized stat difference. Note that these visualizations do not account for how the model is weighing each stats, it's just the normalized difference in the stats between the fighters to give you an idea of where each fighter has an advantage. Larger surface area = better stats but you may notice sometimes the fighter with the larger surface area is not picked, this is due to the fact the stats are not weighed equally by the model and also because the model makes some complex relationships between the stats that won't be reflected by the visualization.

Based on the past 2 months of performance I'm fairly convinced I have some bugs in the nonunit tested code. I've started the unit testing but I'm not done yet so take this event (3-1-2025 UFC Fight Night) with a grain of salt, might be a good one to skip for now, but I should have lots of time after work to finish unit testing next week and I'll post an update about bugs found once I'm done.

After countless hours of trial and error testing this week, we're implementing a few key refinements to the model. Rather than making sweeping changes, we're focusing on targeted improvements that have shown consistent benefits in our testing:

1. Updated Training Data Window

We're moving the cutoff date for training data from 2014 to 2016. While I've been using 2014 as the starting point for the past 4 years, it's time to shift forward to better capture recent trends in the sport. MMA evolves rapidly, and data from 10 years ago may not be as relevant to today's fighting landscape as it once was.

2. New Feature: UFC Age

We've added a simple but effective new stat: UFCAge. This measures the amount of time a fighter has been in the UFC. While straightforward, this metric helps capture valuable information about a fighter's experience at the highest level of competition.

3. Enhanced Feature Layering

Previously, we were using two primary layers of features:

• Decayed adjusted performance (dec_adjperf_dec_avg)
• Opponents' decayed average (opp_dec_avg)

Now we're adding a third layer: the fighter's individual stats (like strikes_landed_ratio_dec_avg). This addition has proven valuable - by combining all three layers of a key base stat (like head_landed_ratio), the algorithm seems better equipped to predict how each fighter will perform relative to the broader UFC population.

Looking Forward

I'm preparing to start producing analysis videos to help explain the model's decision-making process and break down specific fight predictions. The site has been updated with the latest calibration curve, model evaluations, and feature importance rankings to reflect these changes.

As always, these updates are focused on one goal: improving our ability to predict fight outcomes accurately. The changes might seem subtle, but in the world of fight prediction, small edges often make the difference.

Goddamn that took forever. There was a bug in the zscore normalization stat I named _adjperf. If you recall, the calculation for adjperf is:

stat_adjperf = (fighter1_stat - fighter2_prev_fight_stat_opp_avg) / fighter2_prev_fight_stat_opp_sdev

• f2_stat_opp_avg is the historical opponent average against fighter2 pulled from fighter2's previous fight.
• f2_stat_opp_sdev is the historical opponent standard deviation pulled from fighter2's previous fight.

This stat is extremely complicated to implement and was the reason we were predicting so few fights ever since v5 was released with it included. We train with only data known pre-fight so we shift all the data backwards by 1 fight for all fighters. The consequences:

Case #1:

All fights where at least one fighter is debuting are immediately eliminated because their data is 100% null after we shift the data backwards by 1 fight and we can make no comparisons between them and their opponent.

Case #2:

All fights where at least one fighter has only 1 previous fight is useless because one-previous-fight fighter has a 0 in fighter2_prev_fight_stat_opp_sdev for their opponent's adjperf calculation.

Case #3

One fighter has 3 previous fights, the other fighter has 2. Again, adjusted_performance for fighter1 will be 0.

And so on. It means that _adjperf is causing an enormous amount of fights to be dropped.

I've tried to fix this by calculating an initial standard deviation for all first time fighters. I collect all stats of first-time fighters on a per weightclass, per stat basis. So your _adjperf score against first-time fighters is based on how good or bad you did compared to the median first time fighter's stats. This feels fine, because we're dropping all fights where either fighter only has 2 previous fights anyway.

Bug Fixes

So there was a fun little bug affecting ~2% of the training data where fighter2_stat_opp_sdev would end up being 0.00000002 or something so the adjperf score would end up being like 11,839,902 instead of a more normal 1.5 or -1 (i.e., fighter1 scored 1.5 standard deviations above what fighter2 usually allows in that stat from their historical opponents). The reason was because I only use time-decayed averages in the final model to capture recent trends in both fighters and their opponents and the time-decayed standard deviation calculation is a bit complex:

weight = EXP(-λ * ((T - t) / 365.25))

Sooooooometimes, T = 7.777777777 and t = 77.77777778 due to rounding in Postgres double precision. I have fixed this by capping the minimum standard deviation of stats to their 5th percentile. This is to avoid insane standard deviations in tiny edge cases like Khamzat Chimaev's early UFC run where his opponents only scored like 4 strikes against him in 4 fights then he fought Gilbert Burns who hit him 223 times. This meant Burns' _adjperf score was insane because he took Khamzat like 400 standard deviations away from his previous opponent averages.

Last, I had some small bugs affecting the filtering of training data. The order of filtering the data matters a LOT and I was doing some dumb stuff like filtering out Draws and stuff, THEN calculating number of fights for each fighter and filtering on number of fights which is wrong because I already filtered out fights before calculating number of fights for each fighter.

OK! That about wraps up the updates this week. It took a really long time to get through all those bugs so I'm trying to get the updated predictions out before this event, bear with me.

First, we're changing the wording from "AI win%" to "AI confidence". This is to sort out the confusion that many traditional bettors have. This algo is not specialized in finding +EV. It is a binary classification algorithm, meaning it is very good at figuring out who will win, but not the real world win % chance. Predictor.predict(upcoming_fights) returns a binary value of 1 = fighter1 predicted to win, 0 = fighter1 predicted to lose. We can do predictor.predict_proba(upcoming_fights) and get it's best guess at each fighter's implied probability but generally this probability is not well-calibrated because this is specifically a binary classifier.

Second, the reason we're doing parlays is because they're essentially a multiplier of the profit from the single picks. You can risk less units to win more. You don't have to do this, you can just do the straight picks and limit the boom and bust cycle of the parlay strategy, but backtesting is showing the parlay strategy consistently outperforms the straight picks in ROI.

On this note, up until now I've been randomly creating the parlays. I've been trying to figure out how to get rid of that randomization. Sorting the fights by AI confidence or inconfidence ended up performing worse than random picks. So I thought about what does the algorithm crave to become more accurate? Data.

The new parlay strategy is based on backtesting showing more consistent results by sorting the parlays by total combined fights both fighters have had. Islam has had 15 fights in the UFC. Renato Moicano has had 17 fights. That's 32 fights of data that the algorithm has had time to calibrate on. So whatever the algorithm picks on this fight is likely to have the most consistent accuracy. That's why we're seeing islam in 3 parlays this event.

This strategy could use more refinement, and ideally we'd actually just create every possible 3 leg parlay and set that up as the predictions for every event. The only reason I don't do that is because it takes forever to input all those parlays into betmma.tips and the bookie but maybe once I automate the placing of pre-event picks into betmma.tips or something then I'll start doing all parlay combinations possible as the recommended picks.

Alright, so I'm finally ready to talk about my new key feature: Adjusted Performance. This has been one of those "why didn't I think of this sooner" moments, but also "holy crap this is a nightmare to implement." Let me give you a quick taste of what it looks like mathematically:

fighter1_stat_adjperf = (fighter1_stat − fighter2_stat_opp_avg) / fighter2_stat_opp_sdev

We'll call this f1_stat_adjperf for short. The big idea is to measure how much a fighter's performance in any given fight exceeded or fell short of what we'd expect their opponent to allow. If you go in there against some unstoppable jab machine who normally forces everyone to eat 50 jabs per round, but you manage to hold them to only 20, well, that's huge. But if you never do the math to figure out what your opponent's "baseline" is, you'll just record "Fighter1 absorbed 20 jabs" and maybe think it's not that great. Meanwhile, that's incredibly good compared to the 50 jabs everyone else took. Hence, adjusted performance.

Understanding the _opp Suffix

Before going any further, let's talk about the _opp suffix. First, _opp is the post-fight stats your opponent did against you. So if you see something like f2_stat_opp_avg, that means the stat is referencing "what your opponent's opponents did against them." For example:

• f1_stat_opp_avg: The average of your opponents' performances against you in all their fights.
• f2_stat_opp_avg: The average of your opponent's opponents' performances against your opponent in all their previous fights.
• f2_stat_opp_sdev: The standard deviation of your opponent's opponents performance in those same fights, giving us a measure of the volatility or variability in their performance.

So, if your opponent has 40 strikes landed against them then f2_strikes_opp_avg is 40.

This means, to measure your adjusted performance, you compare your post-fight stat in the fight to their pre-fight _opp_avg, and then scale it by pre-fight _opp_sdev. If you get 60 strikes against someone who averages getting hit 30 times, you're 1 standard deviation above average against that person.

Why It's So Valuable

Let's be honest: raw stats can lie, or at least mislead. If a fighter's output is just "I landed 30 strikes," that doesn't tell me how many strikes they should have been able to land. If they were fighting an iron-clad defensive wizard who typically only allows 10 strikes, then landing 30 is insane. On the flip side, if your opponent is basically an open punching bag who gives up 60 strikes on average, then landing 30 is actually pretty weak.

Adjusted performance changes the game: it says, "30 strikes might be good or bad, but let's see how it compares to what your opponent usually allows." Then, for even more nuance, it's scaled by the opponent's historical standard deviation—so you don't artificially inflate your stats just because you faced someone with wide variability on a certain stat.

The Complexity: Where Do You Even Get These Numbers?

The problem with pulling off something like f1_stat_adjperf is that you actually have to calculate your opponent's _opp_avg and _opp_sdev. In other words:

• Grab all your opponent's previous fights.
• For each of those fights, figure out the stats they allowed to their opponents.
• From that, compute the average allowed stats and the standard deviation of those stats.
• Then bring that back into your current fight to see how well or poorly you did.

This is where the data pipeline can get insane, because you might have a fighter who has 15 or 20 fights, each with a different set of opponents. Some of those opponents have 30 fights apiece. Doing this for every fighter means you need to traverse a huge web of fight stats.

If you run a naive approach—like just using Panda's groupby and merges all day—it becomes unbelievably slow at scale. This is why I had to do some major refactoring, rewriting a chunk of my data pipeline to pull from a properly indexed database (Postgres, in my case). Once your data is properly structured, it's much faster to do these calculations in a single pass or via specialized queries, rather than stumbling around in memory merges.

Time-Decayed Averages & Time-Decayed StdDev

But wait—there's more. I decided to do a time-decayed average (and corresponding standard deviation) with a 1.5-year half-life. That means that a fight 3 months ago is given a lot more weight than a fight 5 years ago, which is basically ancient history in fight years.

Now the complexity is multiplied by, like, a factor of 10. Because to get f2_stat_opp_avg, I can't just average everything your opponent has done; I have to:

• Grab each fight's stat.
• Weight it exponentially based on how recently it happened.
• Sum up those weighted stats.
• Divide by the sum of the weights.
• Then do it all over again for the standard deviation.

And let's not forget: we do this for every single fight, across thousands of fights, across hundreds of fighters. That's why I always say data engineering is half the battle.

Why Bother?

So why go through this code-wrangling fiasco when your standard raw stats might be "good enough?" Because fights are context-dependent. If you have a stand-up specialist with insane takedown defense, but no one has tested it in years, your raw stats might not reflect the real picture of how they handle a brand-new style. By blending in adjusted performance stats, you're no longer stuck just describing how many strikes or takedowns a fighter landed; you're describing how well they did compared to what their opponent typically experiences—and you're discounting or boosting older fights according to their recency.

This is how we start to see nuanced differences that no raw stat alone can show. It's the difference between "Fighter A landed 40 strikes" vs. "Fighter A forced a 1.5 standard-deviation drop in Fighter B's typical striking output." That second statement captures so much more power. If you can integrate these insights into your model, you get a far more realistic prediction of how a matchup might turn out.

v5 beta is *might* be done in time for the next event. I'm 100's of hours in. The data processing and model training is basically done, I just need to figure out the final feature set and do some tuning. Then I need to write the future prediction code for creating and cleaning the data of future fights. Finally, we're beating Vegas accuracy/log loss without including the odds or rating/ranking stats like an Elo score. That's not to say I won't include those in the future, but it's a great sign that the fundamentals of the model are improving. I would like to thank my $200/mo ChatGPT o1 Pro subscription for making this possible. That model absolutely rules at complex code, especially statistics and math.

Here's a recent training run to give you an idea of current levels of performance. This isn't the final model performance, it's just from tinkering with the feature set and training parameters:

Model Performance:
Training log loss: -0.611
Validation log loss: -0.575
Test Log loss: -0.612
Training accuracy: 0.671
Validation accuracy: 0.698
```
Test accuracy: 0.691

Basically, we're seeing somewhere around 68% to 69% accuracy on last year's fights (Vegas is currently about 67% accurate) that the model has never seen before with excellent log loss. Log loss is the ability of the model to accurately predict the chance a fighter will win. For example, if in its training data it predicts 50 fighters to have a 70% chance to win, and those fighters won 68% of the time, then the log loss is nicely calibrated. This is what allows us to check the EV of AI predictions versus Vegas odds.

Changes:

• Total rewrite
  • Switched from just pandas dataframes (SLOW) to Postgres SQL database (FAST)
  • Greatly improved code readability, design, and efficiency for easier future updates
• Features
  • Total feature overhaul
  • Per minute
    • Uses Bayesian Posterior Mean to smooth the outliers, zeros, and noise reduction
  • Accuracy/defense
    • Uses Bayesian smoothing with a Beta prior to smooth the outliers, zeros, and noise reduction
    • Priors are calculated on a historical pre-fight per-weightclass, per-stat basis
  • Ratio
    • Now does bounded ratio to prevent division by zero and outlier ratios
  • Average
    • Now includes time decayed average rather than recent average

The reason we do all this smoothing is because when a fighter attempts 0 submissions and lands 0 submissions, giving them 0% accuracy is an unrealistic measure of what their submission accuracy would've been had they attempted any submissions. With smoothing it looks more like this:

Subs_land / subs_attempted = accuracy
0 / 0 = 20% acc (similar to historical weightclass average submission accuracy)
0 / 1 = 18% acc
0 / 10 = 2% acc
These are just examples, not the actual numbers but you get the idea. It punishes fighters who never land any attempts but doesn't overpunish them which means future stats that are layered on top will be more realistic to their actual performance based on sparse data.

Second, no more recent averages over an arbitrary number of fights or dates. Time decayed averages are where it's at. Set a half life, like 1 year. Fights within this 1 year account for, let's say, 50% of the time decayed average. Fights the year prior account for 25% of the time decayed average, etc. This gives a much more precise measure of the fighter as he stands today rather than letting how he stood 5 years ago affect his current stats.

All of these changes above were nice and showed a moderate increase in the model's reliability. However, the real coup de grace was a final layer of statistical analysis over the stats that solved the following problem: if you fought nothing but cans 20 fights in a row your stats would make you look better than Jon Jones. But if you fought nothing but top flight competition 20 fights in a row, your stats would look average to below average despite the fact you'd crush the can crusher. The main way people have solved this has been ranking or rating systems like Elo scores. While this is pretty effective it doesn't solve the core problem of the fighter's individual fight stats being a kind of isolated measurement of the fighter that lacks perspective. How do you turn these core, fight by fight stats into an interconnected web where each individual fight's stats can inform and affect the stats of other related fights?

I'll go into detail about the exact math I did to solve that problem along with the mathematical implementation of the Bayesian smoothing on my Patreon for subscribers here soon. See you next event, hopefully!

After watching UFC 309 systematically demolish my model's predictions with the precision of a prime Anderson Silva, I've spent the past week in a caffeine-fueled debugging frenzy. Between muttering obscenities at my terminal and questioning my life choices, I've had some genuine epiphanies about AI development that might save others from my particular flavor of statistical hell.

The Problem with Yes-Man AI

Large Language Models are like that friend who encourages your 3 AM business ideas. "A blockchain-based dating app for cats? Brilliant!" This becomes particularly dangerous when you're knee-deep in feature engineering and looking for validation rather than criticism.

After extensive testing, I've discovered something fascinating about GPT o1's mathematical capabilities. While most LLMs give basic statistical approaches, GPT o1 can dive deep into complex statistical problems. But the real breakthrough came from building an AI feedback loop: get statistical approaches from GPT o1, feed them to Claude for implementation (it writes cleaner code), then feed Claude's code back to GPT o1 for validation.

Even debugging has improved. When Claude's code throws an exception, feeding the error back works once. But for persistent issues, asking Claude "what do you need to debug this error?" is far more effective. It responds with diagnostic code that, once fed with real data, leads to actual fixes rather than band-aids.

This iterative process, combined with extensive prompt engineering and lots of sample data to help GPT o1 truly understand the problem domain, has led to the first major mathematical breakthrough in V5's development: our new Bayesian approach to handling fight statistics.

Bayesian Beta Binomial: The Zero Division Solution

This is only one of many many improvements in V5 but I find it super interesting so I'm writing about it and fuck you if you don't want to hear about it. Let's dive deep into how we handle the dreaded divide-by-zero problem in fight statistics. When calculating success rates (like submission accuracy or strike accuracy), we use Bayesian Beta Binomial analysis to provide meaningful priors that smoothly handle edge cases.

The approach works like this: Instead of naive division that breaks on zeros, we model each ratio as a Beta distribution where:

• α (alpha) represents successful attempts plus prior successes
• β (beta) represents failed attempts plus prior failures
• The posterior mean (α / (α + β)) gives us our smoothed estimate

For example, with submission accuracy:

submission_accuracy = (submissions + α) / (submission_attempts + α + β)

We determine our priors (α, β) through empirical Bayes by analyzing the historical distribution of success rates across all fighters. These priors vary by stat type, reflecting the different base rates we see in MMA:

• Submissions: Lower α and higher β values reflecting their relative rarity
• Strikes: More balanced α and β values reflecting higher occurrence rates
• Takedowns: Intermediate values based on historical success rates

This approach elegantly handles three critical cases:

• Zero attempts: Returns the prior mean (α/(α+β))
• Small sample sizes: Heavily weights the prior
• Large sample sizes: Converges to the empirical rate

To understand why this matters, consider how submission accuracy was traditionally handled: A fighter attempting 10 submissions and landing none would be assigned 0% accuracy. This creates two problems: it skews averages downward, and when comparing fighters (fighter1_sub_acc / fighter2_sub_acc), we risk another divide-by-zero error.

Our Bayesian approach instead provides more nuanced, realistic estimates. For example:

• 10 attempts, 0 successes = 3.5% accuracy
• 9 attempts, 0 successes = 3.8% accuracy
• 8 attempts, 0 successes = 4.1% accuracy

This prevents over-punishing unsuccessful attempts while ensuring we never hit true zero. The accuracy gradually increases as sample size decreases, reflecting our increasing uncertainty with smaller sample sizes.

The V5 Redemption Arc

For V5, we're continuing to embrace AutoML (specifically AutoGluon) to eliminate the uncertainty in model optimization. Through V1-V3, I spent countless hours manually tuning gradient boosted algorithms like XGBoost and CatBoost. While I learned an enormous amount about hyperparameter optimization and various other tuning, I was never entirely confident I was meeting professional machine learning engineering standards.

AutoML removes that uncertainty. It systematically explores model architectures and hyperparameters in ways that would take me months to do manually. I still do significant tuning, but now it's faster and more reliable. No more wondering if I missed some crucial optimization or made rookie mistakes in the model architecture.

What This Means For Users

MMA-AI.net will continue hosting Model V4 predictions while V5 is under development. However, there won't be any improvements to the current model during this transition. If you want to take a step back and not ride with me for a month or two while I finish V5, I completely understand. This isn't about quick fixes - it's about building something that actually works.

The Bottom Line

Sometimes you need to lose six parlays in a row to light a fire under your ass and actually learn some math. But at least we're failing forward, and V5 will be built on more solid foundations.

P.S. To the UFC 309 fighters: those 3 AM tweets weren't personal. It was just the model and the Monster Energy talking.

I'm absolutely furious. UFC 309 just wiped out 6 units with 6 consecutive parlay losses. After four years of development, countless sleepless nights, and what I thought was a breakthrough in betting strategy, reality hit hard.

The Journey to Version 4

The evolution of MMA-AI.net has been a marathon. Version 1 took two years of meticulous development. When ChatGPT emerged, I saw an opportunity to rebuild everything from the ground up. Version 3 emerged after three months of intense work—I'm talking 5 AM bedtimes, night after night.

Then came Version 4, inspired by Chris from wolftickets.ai. His analysis revealed something fascinating: parlays could be more profitable than single picks when accounting for odds. This insight led to another complete overhaul, this time leveraging autoML to eliminate inefficiencies and using ChatGPT for guidance. The results were stunning: 50-60% ROI over six months.

Success Breeds Complacency

Those six months of success? They made me soft. I coasted. My initial $270 investment had grown to $13,000 purely through profit reinvestment—no additional capital needed. The model was working so well that I focused instead on rebuilding this website using Cursor, an AI-powered IDE. Despite knowing nothing about web development, HTML, or CSS, I managed to transform MMA-AI.net from an ad-riddled eyesore into what you see today.

Traffic surged to all-time highs. Everything seemed perfect. Then UFC 309 happened.

The Wake-Up Call

Six parlays. Six losses. 100% drawdown. The rage I'm feeling isn't just about the money—it's about the realization that I've been resting on my laurels. Those six months of coasting caught up with me in the most painful way possible.

This isn't the end of MMA-AI.net. Honestly, it's just what I needed to get my ass in gear and learn some math. I'm already planning the next evolution.

Stay tuned for my next post about where we go from here.

After three years of development, thousands of hours of feature engineering, and endless testing, I finally redid the stupid website. Goodbye ads, hello pretty new design. This platform represents what I believe to be one of the most sophisticated sports prediction models available today.

The past 5 months have been particularly exciting as we've cracked one of the final pieces of the profit-maximization puzzle: the betting strategy. Chris from wolftickets.ai and I knew there had to be a better approach than simply betting straight picks to maximize ROI. Chris was the first to discover it: parlays.

Since both of our models maintain significant accuracy and log loss advantages over Vegas, we can multiply that edge using parlays. Why? Because parlay odds aren't additive—they're multiplicative. Through extensive testing, we've found that 3-leg parlays offer the optimal balance of risk and reward. While 4-leg parlays actually showed higher ROI in testing, their boom-or-bust nature led to more extreme bankroll swings and higher bankruptcy risk. Since implementing the 3-leg strategy five months ago, the model has achieved a 50% ROI.

The Parlay Strategy

Our approach is straightforward: randomly selected AI picks combined into parlays, with no fighter appearing more than twice to prevent single-fighter dependency. The most common question I get is "Why not just parlay the +EV fighters together?" Well, I've tested hundreds of parlay permutations: underdogs only, favorites only, +EV only, 1-5 leg combinations—every variation imaginable—against a year of unseen fight data. Surprisingly, the +EV-only strategies consistently underperformed compared to randomly selected AI pick parlays.

This might seem counterintuitive, but it likely stems from how we're solving a binary classification problem. Our models excel at distinguishing wins (1) from losses (0), but may be less refined at setting precise win probabilities. I train on log loss, not accuracy—log loss being a metric that heavily penalizes confident mistakes while rewarding confident correct predictions. You can see evidence of this in the calibration curve on our About page.

But honestly? I don't care about the "why." Too many people get tunnel vision focusing on EV, which makes sense if you're working without a mathematical model like MMA-AI.net. But when you have a proven model with demonstrable advantages over Vegas odds, the only metric that matters is ROI. And our testing shows that random AI pick parlays consistently deliver the highest returns.

So here's to the new site, the new strategy, and the new model. You can find my predictions posted here on the home page and occasionally on Twitter/X or https://reddit.com/r/mmabetting before each event.